
Quaternion-Kähler manifold
Encyclopedia
In differential geometry, a quaternion-Kähler manifold (or quaternionic Kähler manifold) is a Riemannian manifold whose Riemannian holonomy group
is a subgroup of Sp(n)·Sp(1).
Another, more explicit, definition, uses a 3-dimensional subbundle H of End(TM) of endomorphisms of the tangent bundle to a Riemannian M. For M to be quaternion-Kähler, H should be preserved by the Levi-Civita connection and pointwise isomorphic to the imaginary quaternions, in such a way that unit imaginary quaternions in H act on TM preserving the metric.
Notice that this definition includes hyperkähler manifold
s. However, these are often excluded from the definition of a quaternion-Kähler manifold by imposing the condition that the scalar curvature
is nonzero, or that the holonomy group is equal to Sp(n)·Sp(1).
as the only manifolds of special holonomy with
non-zero Ricci curvature. In fact, these manifolds are Einstein
.
If an Einstein constant of a quaternion-Kähler manifold is zero, it is hyperkähler
. This case is often excluded from the definition. That is, quaternion-Kähler is defined as one with holonomy reduced to Sp(n)·Sp(1) and with non-zero Ricci curvature (which is constant).
Quaternion-Kähler manifolds divide naturally into those with positive and negative Ricci curvature.

Here, SU(2) is the subgroup associated with the highest root of G, and K0 is its centralizer in G. The Wolf spaces with positive Ricci curvature are compact and simply connected.
If G is Sp(n+1), the corresponding Wolf space is the quaternionic projective space
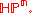
It can be identified with a space of quaternionic lines in Hn+1.
It is conjectured that all quaternion-Kähler manifolds with positive Ricci curvature are symmetric.
methods of twistor theory (this approach is due to Penrose and Salamon). Let M be a quaternionic-Kähler manifold, and H the corresponding subbundle of End(TM), pointwise isomorphic to the imaginary quaternions. Consider the corresponding S2-bundle
S of all h in H satisfying h2 = -1. The points of S are identified with the complex structures on its base. Using this, it is can be shown that the total space Z of S is equipped with an almost complex structure
.
Salamon proved that this almost complex structure is integrable, hence Z is a complex manifold. When the Ricci curvature of M is positive, Z is a projective Fano manifold
, equipped with a holomorphic contact structure.
The converse is also true: a projective Fano manifold which admits a holomorphic contact structure is always a twistor space, hence quaternion-Kähler geometry with positive Ricci curvature is essentially equivalent to the geometry of holomorphic contact Fano manifolds.
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
is a subgroup of Sp(n)·Sp(1).
Another, more explicit, definition, uses a 3-dimensional subbundle H of End(TM) of endomorphisms of the tangent bundle to a Riemannian M. For M to be quaternion-Kähler, H should be preserved by the Levi-Civita connection and pointwise isomorphic to the imaginary quaternions, in such a way that unit imaginary quaternions in H act on TM preserving the metric.
Notice that this definition includes hyperkähler manifold
Hyperkähler manifold
In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp(k) In differential geometry, a hyperkähler...
s. However, these are often excluded from the definition of a quaternion-Kähler manifold by imposing the condition that the scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
is nonzero, or that the holonomy group is equal to Sp(n)·Sp(1).
Ricci curvature
Quaternion-Kähler manifolds appear in Berger's list of Riemannian holonomiesHolonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
as the only manifolds of special holonomy with
non-zero Ricci curvature. In fact, these manifolds are Einstein
Einstein manifold
In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric...
.
If an Einstein constant of a quaternion-Kähler manifold is zero, it is hyperkähler
Hyperkähler manifold
In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp In differential geometry, a hyperkähler manifold is a Riemannian manifold of dimension 4k and holonomy group contained in Sp(k) In differential geometry, a hyperkähler...
. This case is often excluded from the definition. That is, quaternion-Kähler is defined as one with holonomy reduced to Sp(n)·Sp(1) and with non-zero Ricci curvature (which is constant).
Quaternion-Kähler manifolds divide naturally into those with positive and negative Ricci curvature.
Examples
There are no known examples of compact quaternion-Kähler manifolds which are not locally symmetric or hyperkähler. Symmetric quaternion-Kähler manifolds are also known as Wolf spaces. For any simple Lie group G, there is a unique Wolf space G/K obtained as a quotient of G by a subgroup
Here, SU(2) is the subgroup associated with the highest root of G, and K0 is its centralizer in G. The Wolf spaces with positive Ricci curvature are compact and simply connected.
If G is Sp(n+1), the corresponding Wolf space is the quaternionic projective space
Quaternionic projective space
In mathematics, quaternionic projective space is an extension of the ideas of real projective space and complex projective space, to the case where coordinates lie in the ring of quaternions H. Quaternionic projective space of dimension n is usually denoted byand is a closed manifold of dimension 4n...
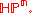
It can be identified with a space of quaternionic lines in Hn+1.
It is conjectured that all quaternion-Kähler manifolds with positive Ricci curvature are symmetric.
Twistor spaces
Questions about quaternion-Kähler manifolds of positive Ricci curvature can be translated into the language of algebraic geometry using themethods of twistor theory (this approach is due to Penrose and Salamon). Let M be a quaternionic-Kähler manifold, and H the corresponding subbundle of End(TM), pointwise isomorphic to the imaginary quaternions. Consider the corresponding S2-bundle
S of all h in H satisfying h2 = -1. The points of S are identified with the complex structures on its base. Using this, it is can be shown that the total space Z of S is equipped with an almost complex structure
Almost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
.
Salamon proved that this almost complex structure is integrable, hence Z is a complex manifold. When the Ricci curvature of M is positive, Z is a projective Fano manifold
Fano variety
In algebraic geometry, a Fano variety, introduced by , is a non-singular complete variety whose anticanonical bundle is ample.Fano varieties are quite rare, compared to other families, like Calabi–Yau manifolds and general type surfaces....
, equipped with a holomorphic contact structure.
The converse is also true: a projective Fano manifold which admits a holomorphic contact structure is always a twistor space, hence quaternion-Kähler geometry with positive Ricci curvature is essentially equivalent to the geometry of holomorphic contact Fano manifolds.

