Queue machine
Encyclopedia
A queue machine or queue automaton is a finite state machine
with the ability to store and retrieve data from an infinite-memory queue. It is a model of computation equivalent to a Turing machine
, and therefore it can process any formal language
.
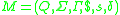where
We define the current status of the machine by a configuration, an ordered pair of its state and queue contents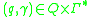
(note 
defines the Kleene closure or set of all supersets of 
). Therefore the starting configuration on an input string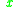 
is defined as 
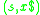, and we can define our transition as the function that, given an initial state and queue, takes the function to a new state and queue. Note the "first-in-first-out" property of the queue in the relation
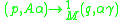
where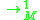
defines the next configuration relation, or simply the transition function from one configuration to the next.
The machine accepts a string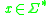
if after a (possibly infinite) number of transitions the starting configuration evolves to exhaust the string (reaching a null string 
), or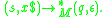 
A Turing machine can be simulated by a queue machine that keeps a copy of the Turing machine's contents in its queue at all times, with two special markers: one for the TM's head position, and one for the end of the tape; its transitions simulate those of the TM by running through the whole queue, popping off each of its symbols and re-enqueing either the popped symbol, or, near the head position, the equivalent of the TM transition's effect.
A queue machine can be simulated by a Turing machine, but more easily by a multi-tape Turing machine, which is known to be equivalent to a normal single-tape machine.
The simulating queue machine reads input on one tape and stores the queue on the second, with pushes and pops defined by simple transitions to the beginning and end symbols of the tape. A formal proof of this is often an exercise in theoretical computer science courses.
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
with the ability to store and retrieve data from an infinite-memory queue. It is a model of computation equivalent to a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
, and therefore it can process any formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
.
Theory
We define a queue machine by the six-tupl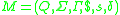e where-
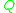is a finite set of states; -
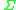is the finite set of the input alphabet; -
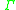is the finite queue alphabet; -
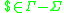is the initial queue symbol; -
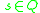is the start state; -
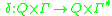is the transition function.
We define the current status of the machine by a configuration, an ordered pair of its state and queue contents
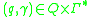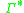(note defines the Kleene closure or set of all supersets of 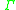). Therefore the starting configuration on an input string 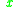is defined as 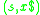, and we can define our transition as the function that, given an initial state and queue, takes the function to a new state and queue. Note the "first-in-first-out" property of the queue in the relation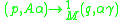where
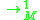defines the next configuration relation, or simply the transition function from one configuration to the next.The machine accepts a string
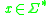if after a (possibly infinite) number of transitions the starting configuration evolves to exhaust the string (reaching a null string ), or 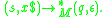Turing completeness
We can prove that a queue machine is equivalent to a Turing machine by showing that a queue machine can simulate a Turing machine and vice-versa.A Turing machine can be simulated by a queue machine that keeps a copy of the Turing machine's contents in its queue at all times, with two special markers: one for the TM's head position, and one for the end of the tape; its transitions simulate those of the TM by running through the whole queue, popping off each of its symbols and re-enqueing either the popped symbol, or, near the head position, the equivalent of the TM transition's effect.
A queue machine can be simulated by a Turing machine, but more easily by a multi-tape Turing machine, which is known to be equivalent to a normal single-tape machine.
The simulating queue machine reads input on one tape and stores the queue on the second, with pushes and pops defined by simple transitions to the beginning and end symbols of the tape. A formal proof of this is often an exercise in theoretical computer science courses.
Applications
Queue machines offer a simple model on which to base computer architectures, programming languages, or algorithms.See also
- Computability
- Turing machine equivalentsTuring machine equivalentsThe following article is a referral from the article Turing machine. Many of the machines described here have articles that offer much more information.- Machines equivalent to the Turing machine model :Turing equivalence:...
- Deterministic finite-state machine
- Pushdown automatonPushdown automatonIn automata theory, a pushdown automaton is a finite automaton that can make use of a stack containing data.- Operation :Pushdown automata differ from finite state machines in two ways:...
- Tag systemTag systemA tag system is a deterministic computational model published by Emil Leon Post in 1943 as a simple form of Post canonical system. A tag system may also be viewed as an abstract machine, called a Post tag machine —briefly, a finite state machine whose only tape is a FIFO queue of unbounded length,...
- Manufactoria, a browser flash game tasking the player with implementation of various algorithms using a queue machine model.