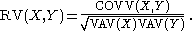RV coefficient
Encyclopedia
In statistics, the RV coefficient
is a multivariate
generalization of the Pearson correlation coefficient.
It measures the closeness of two set of points that may each be represented in a matrix
.
The major approaches within statistical multivariate data analysis
can all be brought into a common framework in which the RV coefficient is maximised subject to relevant constraints. Specifically, these statistical methodologies include:
One application of the RV coefficient is in functional neuroimaging
where it can measure
the similarity between two subjects' series of brain scans
or between different scans of a same subject.
concerning the definition of scalar-valued quantities which are called the "variance" and "covariance" of vector-valued random variables. Note that standard usage is to have matrices for the variances and covariances of vector random variables.
Given these innovative definitions, the RV-coefficient is then just the correlation coefficient defined in the usual way.
Suppose that X and Y are matrices of centered random vectors (column vectors) with covariance matrix given by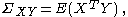
then the scalar-valued covariance (denoted by COVV) is defined by
The scalar-valued variance is defined correspondingly: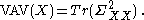
With these definitions, the variance and covariance have certain additive properties in relation to the formation of new vector quantities by extending an existing vector with the elements of another.
Then the RV-coefficient is defined by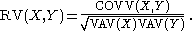
is a multivariate
Multivariate statistics
Multivariate statistics is a form of statistics encompassing the simultaneous observation and analysis of more than one statistical variable. The application of multivariate statistics is multivariate analysis...
generalization of the Pearson correlation coefficient.
It measures the closeness of two set of points that may each be represented in a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
.
The major approaches within statistical multivariate data analysis
Multivariate statistics
Multivariate statistics is a form of statistics encompassing the simultaneous observation and analysis of more than one statistical variable. The application of multivariate statistics is multivariate analysis...
can all be brought into a common framework in which the RV coefficient is maximised subject to relevant constraints. Specifically, these statistical methodologies include:
- principal component analysis
- canonical correlation analysis
- multivariate regressionRegression analysisIn statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
- statistical classification (linear discriminationLinear discriminant analysisLinear discriminant analysis and the related Fisher's linear discriminant are methods used in statistics, pattern recognition and machine learning to find a linear combination of features which characterizes or separates two or more classes of objects or events...
).
One application of the RV coefficient is in functional neuroimaging
Functional neuroimaging
Functional neuroimaging is the use of neuroimaging technology to measure an aspect of brain function, often with a view to understanding the relationship between activity in certain brain areas and specific mental functions...
where it can measure
the similarity between two subjects' series of brain scans
or between different scans of a same subject.
Definitions
The definition of the RV-coefficient makes use of ideasconcerning the definition of scalar-valued quantities which are called the "variance" and "covariance" of vector-valued random variables. Note that standard usage is to have matrices for the variances and covariances of vector random variables.
Given these innovative definitions, the RV-coefficient is then just the correlation coefficient defined in the usual way.
Suppose that X and Y are matrices of centered random vectors (column vectors) with covariance matrix given by
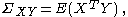
then the scalar-valued covariance (denoted by COVV) is defined by

The scalar-valued variance is defined correspondingly:
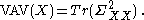
With these definitions, the variance and covariance have certain additive properties in relation to the formation of new vector quantities by extending an existing vector with the elements of another.
Then the RV-coefficient is defined by