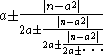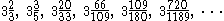Rafael Bombelli
Encyclopedia
Rafael Bombelli was an Italian
mathematician
.
Born in Bologna
, he is the author of a treatise on algebra
and is a central figure in the understanding of imaginary number
s.
He was the one who finally managed to address the problem with imaginary numbers. In his 1572 book, L'Algebra, Bombelli solved equations using the method of del Ferro
/Tartaglia
. He introduced the rhetoric that preceded the representative symbols +i and -i and described how they both worked.
The lunar crater Bombelli
is named after him.
. He was born to Antonio Mazzoli, a wool merchant, and Diamante Scudieri, a tailor's daughter. The Mazzoli family was once quite powerful in Bologna. When Pope Julius II
came to power, in 1506, he exiled the ruling family, the Bentivoglios. The Bentivoglio family attempted to retake Bologna in 1508, but failed. Rafael's grandfather participated in the coup attempt, and was captured and executed. Later, Antonio was able to return to Bologna, having changed his surname to Bombelli to escape the reputation of the Mazzoli family. Rafael was the oldest of six children. Rafael received no college education, but was instead taught by an engineer-architect by the name of Pier Francesco Clementi.
Rafael Bombelli felt that none of the works on algebra by the leading mathematicians of his day provided a careful and thorough exposition of the subject. Instead of another convoluted treatise that only mathematicians could comprehend, Rafael decided to write a book on algebra that could be understood by anyone. His text would be self-contained and easily read by those without higher education.
Rafael Bombelli died in 1572 in Rome, Italy.
http://mata.gia.rwth-aachen.de/Vortraege/Sabrina_Mueller/Geschichte_der_Zahlen/Bilder/cardano.png
"Plus times plus makes plus
Minus times minus makes plus
Plus times minus makes minus
Minus times plus makes minus
Plus 8 times plus 8 makes plus 64
Minus 5 times minus 6 makes plus 30
Minus 4 times plus 5 makes minus 20
Plus 5 times minus 4 makes minus 20"
As was intended, Bombelli used simple language as can be seen above so that anybody could understand it. But at the same time, he was thorough.
Perhaps more importantly than his work with algebra, however, the book also includes Bombelli's monumental contributions to complex number theory. Before he writes about complex numbers, he points out that they occur in solutions of equations of the form x^3 = ax + b, given that (a/3)^3 > (b/2)^2, which is another way of stating that the discriminant of the cubic is negative. The solution of this kind of equation requires taking the cube root of some number and adding the square root of some negative number.
Before Bombelli delves into using imaginary numbers practically, he goes into a detailed explanation of the properties of complex numbers. Right away, he makes it clear that the rules of arithmetic for imaginary numbers are not the same as for real numbers. This was a big accomplishment, as even numerous subsequent mathematicians were extremely confused on the topic.
Bombelli avoided confusion by giving a special name to square roots of negative numbers, instead of just trying to deal with them as regular radicals like other mathematicians did. This made it clear that these numbers were neither positive nor negative. This kind of system avoids the confusion that Euler encountered. Bombelli called the imaginary number i “plus of minus” or “minus of minus” for -i.
Bombelli had the foresight to see that imaginary numbers were crucial and necessary to solving quartic and cubic equations. At the time, people cared about complex numbers only as tools to solve practical equations. As such, Bombelli was able to get solutions using Scipione del Ferro's rule, even in the irreducible case, where other mathematicians such as Cardano had given up.
In his book, Bombelli explains complex arithmetic as follows:
"Plus by plus of minus, makes plus of minus.
Minus by plus of minus, makes minus of minus.
Plus by minus of minus, makes minus of minus.
Minus by minus of minus, makes plus of minus.
Plus of minus by plus of minus, makes minus.
Plus of minus by minus of minus, makes plus.
Minus of minus by plus of minus, makes plus.
Minus of minus by minus of minus makes minus."
After dealing with the multiplication of real and imaginary numbers, Bombelli goes on to talk about the rules of addition and subtraction. He is careful to point out that real parts add to real parts, and imaginary parts add to imaginary parts.
Bombelli is generally regarded as the inventor of complex numbers, as no one before him had made rules for dealing with such numbers, and no one believed that working with imaginary numbers would have useful results. Upon reading Bombelli's Algebra, Leibniz praised Bombelli as an ". . . outstanding master of the analytical art." Crossley writes in his book, "Thus we have an engineer, Bombelli, making practical use of complex numbers perhaps because they gave him useful results, while Cardan found the square roots of negative numbers useless. Bombelli is the first to give a treatment of any complex numbers. . . It is remarkable how thorough he is in his presentation of the laws of calculation of complex numbers. . ."
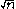begins with 
with 
, from which it can be shown that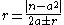 
. Repeated substitution of the expression on the right hand side for 
into itself yields a continued fraction
for the root but Bombelli is more concerned with better approximations for
. The value chosen for 
is either of the whole numbers whose squares 
lies between. The method gives the following convergents
for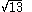
while the actual value is 3.605551275... :
The last convergent equals 3.605550883... . Bombelli's method should be compared with formulas and results used by Heros and Archimedes
. The result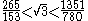
used by Archimedes in his determination of the value of 
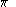can be found by using 1 and 0 for the initial values of 
.
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
.
Born in Bologna
Bologna
Bologna is the capital city of Emilia-Romagna, in the Po Valley of Northern Italy. The city lies between the Po River and the Apennine Mountains, more specifically, between the Reno River and the Savena River. Bologna is a lively and cosmopolitan Italian college city, with spectacular history,...
, he is the author of a treatise on algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and is a central figure in the understanding of imaginary number
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
s.
He was the one who finally managed to address the problem with imaginary numbers. In his 1572 book, L'Algebra, Bombelli solved equations using the method of del Ferro
Scipione del Ferro
Scipione del Ferro was an Italian mathematician who first discovered a method to solve the depressed cubic equation.-Life:Scipione del Ferro was born in Bologna, in northern Italy, to Floriano and Filippa Ferro...
/Tartaglia
Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia was a mathematician, an engineer , a surveyor and a bookkeeper from the then-Republic of Venice...
. He introduced the rhetoric that preceded the representative symbols +i and -i and described how they both worked.
The lunar crater Bombelli
Bombelli (crater)
Bombelli is a small lunar impact crater that is located in the highlands to the north of the Sinus Successus. It was previously designated Apollonius T before being named by the IAU. The crater Apollonius is located to the east-southeast....
is named after him.
Life
Rafael Bombelli was baptised on 20 January 1526 in Bologna, Papal StatesPapal States
The Papal State, State of the Church, or Pontifical States were among the major historical states of Italy from roughly the 6th century until the Italian peninsula was unified in 1861 by the Kingdom of Piedmont-Sardinia .The Papal States comprised territories under...
. He was born to Antonio Mazzoli, a wool merchant, and Diamante Scudieri, a tailor's daughter. The Mazzoli family was once quite powerful in Bologna. When Pope Julius II
Pope Julius II
Pope Julius II , nicknamed "The Fearsome Pope" and "The Warrior Pope" , born Giuliano della Rovere, was Pope from 1503 to 1513...
came to power, in 1506, he exiled the ruling family, the Bentivoglios. The Bentivoglio family attempted to retake Bologna in 1508, but failed. Rafael's grandfather participated in the coup attempt, and was captured and executed. Later, Antonio was able to return to Bologna, having changed his surname to Bombelli to escape the reputation of the Mazzoli family. Rafael was the oldest of six children. Rafael received no college education, but was instead taught by an engineer-architect by the name of Pier Francesco Clementi.
Rafael Bombelli felt that none of the works on algebra by the leading mathematicians of his day provided a careful and thorough exposition of the subject. Instead of another convoluted treatise that only mathematicians could comprehend, Rafael decided to write a book on algebra that could be understood by anyone. His text would be self-contained and easily read by those without higher education.
Rafael Bombelli died in 1572 in Rome, Italy.
http://mata.gia.rwth-aachen.de/Vortraege/Sabrina_Mueller/Geschichte_der_Zahlen/Bilder/cardano.png
Bombelli's Algebra
In the book that he wrote in 1572, entitled Algebra, Bombelli gave a comprehensive account of the algebra known at the time. He was the first to write down how to perform computations with negative numbers. The following is an excerpt from the text:"Plus times plus makes plus
Minus times minus makes plus
Plus times minus makes minus
Minus times plus makes minus
Plus 8 times plus 8 makes plus 64
Minus 5 times minus 6 makes plus 30
Minus 4 times plus 5 makes minus 20
Plus 5 times minus 4 makes minus 20"
As was intended, Bombelli used simple language as can be seen above so that anybody could understand it. But at the same time, he was thorough.
Perhaps more importantly than his work with algebra, however, the book also includes Bombelli's monumental contributions to complex number theory. Before he writes about complex numbers, he points out that they occur in solutions of equations of the form x^3 = ax + b, given that (a/3)^3 > (b/2)^2, which is another way of stating that the discriminant of the cubic is negative. The solution of this kind of equation requires taking the cube root of some number and adding the square root of some negative number.
Before Bombelli delves into using imaginary numbers practically, he goes into a detailed explanation of the properties of complex numbers. Right away, he makes it clear that the rules of arithmetic for imaginary numbers are not the same as for real numbers. This was a big accomplishment, as even numerous subsequent mathematicians were extremely confused on the topic.
Bombelli avoided confusion by giving a special name to square roots of negative numbers, instead of just trying to deal with them as regular radicals like other mathematicians did. This made it clear that these numbers were neither positive nor negative. This kind of system avoids the confusion that Euler encountered. Bombelli called the imaginary number i “plus of minus” or “minus of minus” for -i.
Bombelli had the foresight to see that imaginary numbers were crucial and necessary to solving quartic and cubic equations. At the time, people cared about complex numbers only as tools to solve practical equations. As such, Bombelli was able to get solutions using Scipione del Ferro's rule, even in the irreducible case, where other mathematicians such as Cardano had given up.
In his book, Bombelli explains complex arithmetic as follows:
"Plus by plus of minus, makes plus of minus.
Minus by plus of minus, makes minus of minus.
Plus by minus of minus, makes minus of minus.
Minus by minus of minus, makes plus of minus.
Plus of minus by plus of minus, makes minus.
Plus of minus by minus of minus, makes plus.
Minus of minus by plus of minus, makes plus.
Minus of minus by minus of minus makes minus."
After dealing with the multiplication of real and imaginary numbers, Bombelli goes on to talk about the rules of addition and subtraction. He is careful to point out that real parts add to real parts, and imaginary parts add to imaginary parts.
Accomplishments
In honor of his accomplishments, a moon crater was named after Bombelli.Bombelli is generally regarded as the inventor of complex numbers, as no one before him had made rules for dealing with such numbers, and no one believed that working with imaginary numbers would have useful results. Upon reading Bombelli's Algebra, Leibniz praised Bombelli as an ". . . outstanding master of the analytical art." Crossley writes in his book, "Thus we have an engineer, Bombelli, making practical use of complex numbers perhaps because they gave him useful results, while Cardan found the square roots of negative numbers useless. Bombelli is the first to give a treatment of any complex numbers. . . It is remarkable how thorough he is in his presentation of the laws of calculation of complex numbers. . ."
Bombelli method
Bombelli used a method related to continued fractions to calculate square roots. His method for finding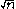 begins with with 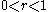, from which it can be shown that 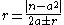. Repeated substitution of the expression on the right hand side for into itself yields a continued fraction
for the root but Bombelli is more concerned with better approximations for
. The value chosen for is either of the whole numbers whose squares lies between. The method gives the following convergentsConvergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
for
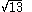while the actual value is 3.605551275... :
The last convergent equals 3.605550883... . Bombelli's method should be compared with formulas and results used by Heros and Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
. The result
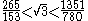used by Archimedes in his determination of the value of can be found by using 1 and 0 for the initial values of .External links
- L'Algebra, Libri I, II, III, IV e V, original Italian texts.
- Background