
Rainbow table
Encyclopedia
A rainbow table is a precomputed table for reversing cryptographic hash function
s, usually for cracking password
hashes. Tables are usually used in recovering the plaintext
password
, up to a certain length consisting of a limited set of characters. It is a form of time-memory tradeoff
, using less CPU at the cost of more storage. Proper key derivation function
s employ a salt
to make this attack infeasible.
Rainbow tables are a refinement of an earlier, simpler algorithm by Martin Hellman
that used the inversion of hashes by looking up precomputed hash chains.
require some way to tell if an entered password is correct. The simplest approach is to store a list of valid passwords, one for each user; however, this allows anyone who gains access to the list to know every user's password. The more common approach is to store a cryptographic hash of the password. This protects the stored information because such hashes are difficult to reverse. However most hashes are designed to be computed quickly. This allows someone who gains access to the stored hash values to rapidly check long lists of possible passwords for validity. One defense against such attacks is to use longer passwords, increasing greatly the number of possible passwords an attacker must check to find the correct one. For simple hash schemes (ones that don't use cryptographic salt), an attacker can precompute the hash values for all common or short passwords and save them in a large table. Once a hash value is obtained it can then be quickly looked up in the table to find the matching password. However as the size of passwords grows, such tables can become too big to store. An alternative is to store the starting points for long chains of hashed passwords. This requires more computation to look up a purloined password hash, but saves greatly on space. Rainbow tables are a refinement on the chaining technique that avoids a technical problem called chain collisions.
s article.
Suppose we have a password hash function H and a finite set of passwords P. The goal is to precompute a data structure that, given any output h of the hash function, can either locate the p in P such that H(p) = h, or determine that there is no such p in P. The simplest way to do this is compute H(p) for all p in P, but then storing the table requires Θ(|P|n) bits of space, where n is the size of an output of H, which is prohibitive for large P.
Hash chains are a technique for decreasing this space requirement. The idea is to define a reduction function R that maps hash values back into values in P. By alternating the hash function with the reduction function, chains of alternating passwords and hash values are formed. For example, if P were the set of lowercase alphabetic 6-character passwords, and hash values were 32 bits long, a chain might look like this:
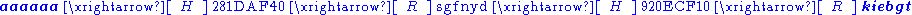
To generate the table, we choose a random set of initial passwords from P, compute chains of some fixed length k for each one, and store only the first and last password in each chain. The first password is called the starting point and the last one is called the endpoint. In the example chain above, "aaaaaa" would be the starting point and "kiebgt" would be the endpoint, and none of the other passwords (or the hash values) would be stored.
Now, given a hash value h that we want to invert (find the corresponding password for), compute a chain starting with h by applying R, then H, then R, and so on. If at any point we observe a value matching one of the endpoints in the table, we get the corresponding starting point and use it to recreate the chain. There's a good chance that this chain will contain the value h, and if so, the immediately preceding value in the chain is the password p that we seek. For example, if we're given the hash 920ECF10, and compute its chain, we would soon reach the password "kiebgt" that is stored in the table:

We then get the corresponding starting password "aaaaaa" and following its chain until 920ECF10 is reached:

The password is "sgfnyd".
Note however that this chain does not always contain the hash value h; it may so happen that the chain starting at h merges with the chain starting at the starting point at some point after h. For example, we may be given a hash value FB107E70, and when we follow its chain, we get kiebgt:

But FB107E70 is not in the chain starting at "aaaaaa". This is called a false alarm. In this case, we ignore the match and continue to extend the chain of h looking for another match. If the chain of h gets extended to length k with no good matches, then the password was never produced in any of the chains.
The table content does not depend on the hash value to be inverted. It is created once and then repeatedly used for the lookups unmodified. Increasing the length of the chain decreases the size of the table. It also increases the time required to perform lookups, and this is the time-memory trade-off of the rainbow table. In a simple case of one-item chains, the lookup is very fast, but the table is very big. Once chains get longer, the lookup slows down, but the table size goes down.
Simple hash chains have several flaws. Most serious if at any point two chains collide (produce the same value), they will merge and consequently the table will not cover as many passwords despite having paid the same computational cost to generate. Because previous chains are not stored in their entirety, this is impossible to detect efficiently. For example, if the third value in chain 3 matches the second value in chain 7, the two chains will cover almost the same sequence of values, but their final values will not be the same. The hash function H is unlikely to produce collisions as it usually considered an important security feature not to do so, but the reduction function R, because of its need to correctly cover the likely plaintexts, can not be collision resistant.
Other difficulties result from the importance of choosing the correct function for R. Picking R to the identity is little better than a brute force approach. Only when the attacker has a good idea of what the likely plaintexts will be can he choose a function R that makes sure only time and space are used for likely plaintexts not the entire space of possible passwords. In effect R shepherds the results of prior hash calculations back to likely plaintexts but this benefit comes with drawback that R likely won't produce every possible plaintext in the class the attacker wishes to check denying certainty to the attacker that no passwords came from his chosen class. Also it can be difficult to design the function R to match the expected distribution of plaintexts.
Using sequences of reduction functions changes how lookup is done: because the hash value of interest may be found at any location in the chain, it's necessary to generate k different chains. The first chain assumes the hash value is in the last hash position and just applies Rk; the next chain assumes the hash value is in the second-to-last hash position and applies Rk−1, then H, then Rk; and so on until the last chain, which applies all the reduction functions, alternating with H. This creates a new way of producing a false alarm: if we "guess" the position of the hash value wrong, we may needlessly evaluate a chain.
Although rainbow tables have to follow more chains, they make up for this by having fewer tables: simple hash chain tables cannot grow beyond a certain size without rapidly becoming inefficient due to merging chains; to deal with this, they maintain multiple tables, and each lookup must search through each table. Rainbow tables can achieve similar performance with tables that are k times larger, allowing them to perform a factor of k fewer lookups.
Rainbow tables use a refined algorithm with a different reduction function for each "link" in a chain, so that when there is a hash collision in two or more chains the chains will not merge as long as the collision doesn't occur at the same position in each chain. As well as increasing the probability of a correct crack for a given table size, this use of multiple reduction functions approximately doubles the speed of lookups. See the paper cited below for details.
Rainbow tables are specific to the hash function they were created for e.g., MD5
tables can crack only MD5 hashes. The theory of this technique was first pioneered by Philippe Oechslin as a fast form of time-memory tradeoff
, which he implemented in the Windows
password cracker
Ophcrack
. The more powerful RainbowCrack
program was later developed that can generate and use rainbow tables for a variety of character sets and hashing algorithms, including LM hash
, MD5
, SHA1, etc..
. For example, consider a password hash that is generated using the following function (where "." is the concatenation
operator):
Or
The salt value is not secret and may be generated at random and stored with the password hash. A large salt value prevents precomputation attacks, including rainbow tables, by ensuring that each user's password is hashed uniquely. This means that two users with the same password will have different password hashes (assuming different salts are used). In order to succeed, an attacker needs to precompute tables for each possible salt value. The salt must be large enough, otherwise an attacker can make a table for each salt value. For older Unix passwords
which used a 12-bit salt this would require 4096 tables, a significant increase in cost for the attacker, but not impractical with terabyte hard drives. The MD5-crypt and bcrypt methods—used in Linux
, BSD Unixes, and Solaris—have salts of 48 and 128 bits, respectively. These larger salt values make precomputation attacks for almost any length of password infeasible against these systems for the foreseeable future.
Another technique that helps prevent precomputation attacks is key stretching. When stretching is used, the salt, password, and a number of intermediate hash values are run through the underlying hash function multiple times to increase the computation time required to hash each password. For instance, MD5-Crypt uses a 1000 iteration loop that repeatedly feeds the salt, password, and current intermediate hash value back into the underlying MD5 hash function. The user's password hash is the concatenation of the salt value (which is not secret) and the final hash. The extra time is not noticeable to a user because the user only has to wait a fraction of a second each time the user logs in. On the other hand, stretching greatly reduces the effectiveness of a brute-force or precomputation attacks because it reduces the number of computations an attacker can perform in a given time frame. This principle is applied in MD5-Crypt and in bcrypt.
An alternative approach, called key strengthening, extends the key with a random salt, but then (unlike in key stretching) securely deletes the salt. This forces both the attacker and legitimate users to perform a brute-force search for the salt value. Although the paper that introduced key stretching referred to this earlier technique and intentionally chose a different name, the term "key strengthening" is now often (arguably incorrectly) used to refer to key stretching.
Rainbow tables and other precomputation attacks do not work against passwords that contain symbols outside the range presupposed, or that are longer than those precomputed by the attacker. However tables can be generated that take into account common ways in which users attempt to choose more secure passwords, such as adding a number or special character. Because of the sizable investment in computing processing, rainbow tables beyond fourteen places in length are not yet common. So, choosing a password that is longer than fourteen characters may force an attacker to resort to brute-force methods.
Certain intensive efforts focused on LM hash
, an older hash algorithm used by Microsoft, are publicly available. LM hash is particularly vulnerable because passwords longer than 7 characters are broken into two sections, each of which is hashed separately. Choosing a password that is fifteen characters or longer guarantees that an LM hash will not be generated.
, Linux
, and BSD use hashes with salts, though many applications use just a hash (typically MD5
) with no salt. The Microsoft Windows NT/2000 family uses the LAN Manager
and NT LAN Manager
hashing method and is also unsalted, which makes it one of the more popularly generated tables.
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
s, usually for cracking password
Password cracking
Password cracking is the process of recovering passwords from data that has been stored in or transmitted by a computer system. A common approach is to repeatedly try guesses for the password...
hashes. Tables are usually used in recovering the plaintext
Plaintext
In cryptography, plaintext is information a sender wishes to transmit to a receiver. Cleartext is often used as a synonym. Before the computer era, plaintext most commonly meant message text in the language of the communicating parties....
password
Password
A password is a secret word or string of characters that is used for authentication, to prove identity or gain access to a resource . The password should be kept secret from those not allowed access....
, up to a certain length consisting of a limited set of characters. It is a form of time-memory tradeoff
Space-time tradeoff
In computer science, a space–time or time–memory tradeoff is a situation where the memory use can be reduced at the cost of slower program execution...
, using less CPU at the cost of more storage. Proper key derivation function
Key derivation function
In cryptography, a key derivation function derives one or more secret keys from a secret value such as a master key or other known information such as a password or passphrase using a pseudo-random function...
s employ a salt
Salt (cryptography)
In cryptography, a salt consists of random bits, creating one of the inputs to a one-way function. The other input is usually a password or passphrase. The output of the one-way function can be stored rather than the password, and still be used for authenticating users. The one-way function...
to make this attack infeasible.
Rainbow tables are a refinement of an earlier, simpler algorithm by Martin Hellman
Martin Hellman
Martin Edward Hellman is an American cryptologist, and is best known for his invention of public key cryptography in cooperation with Whitfield Diffie and Ralph Merkle...
that used the inversion of hashes by looking up precomputed hash chains.
Background
Computer systems that rely on passwords for authenticationAuthentication
Authentication is the act of confirming the truth of an attribute of a datum or entity...
require some way to tell if an entered password is correct. The simplest approach is to store a list of valid passwords, one for each user; however, this allows anyone who gains access to the list to know every user's password. The more common approach is to store a cryptographic hash of the password. This protects the stored information because such hashes are difficult to reverse. However most hashes are designed to be computed quickly. This allows someone who gains access to the stored hash values to rapidly check long lists of possible passwords for validity. One defense against such attacks is to use longer passwords, increasing greatly the number of possible passwords an attacker must check to find the correct one. For simple hash schemes (ones that don't use cryptographic salt), an attacker can precompute the hash values for all common or short passwords and save them in a large table. Once a hash value is obtained it can then be quickly looked up in the table to find the matching password. However as the size of passwords grows, such tables can become too big to store. An alternative is to store the starting points for long chains of hashed passwords. This requires more computation to look up a purloined password hash, but saves greatly on space. Rainbow tables are a refinement on the chaining technique that avoids a technical problem called chain collisions.
Precomputed hash chains
Note: The hash chains described in this article are a different kind of chain than those described in the hash chainHash chain
A hash chain is the successive application of a cryptographic hash function to a piece of data. In computer security, a hash chain is a method to produce many one-time keys from a single key or password...
s article.
Suppose we have a password hash function H and a finite set of passwords P. The goal is to precompute a data structure that, given any output h of the hash function, can either locate the p in P such that H(p) = h, or determine that there is no such p in P. The simplest way to do this is compute H(p) for all p in P, but then storing the table requires Θ(|P|n) bits of space, where n is the size of an output of H, which is prohibitive for large P.
Hash chains are a technique for decreasing this space requirement. The idea is to define a reduction function R that maps hash values back into values in P. By alternating the hash function with the reduction function, chains of alternating passwords and hash values are formed. For example, if P were the set of lowercase alphabetic 6-character passwords, and hash values were 32 bits long, a chain might look like this:
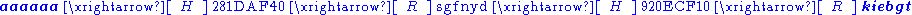
To generate the table, we choose a random set of initial passwords from P, compute chains of some fixed length k for each one, and store only the first and last password in each chain. The first password is called the starting point and the last one is called the endpoint. In the example chain above, "aaaaaa" would be the starting point and "kiebgt" would be the endpoint, and none of the other passwords (or the hash values) would be stored.
Now, given a hash value h that we want to invert (find the corresponding password for), compute a chain starting with h by applying R, then H, then R, and so on. If at any point we observe a value matching one of the endpoints in the table, we get the corresponding starting point and use it to recreate the chain. There's a good chance that this chain will contain the value h, and if so, the immediately preceding value in the chain is the password p that we seek. For example, if we're given the hash 920ECF10, and compute its chain, we would soon reach the password "kiebgt" that is stored in the table:

We then get the corresponding starting password "aaaaaa" and following its chain until 920ECF10 is reached:

The password is "sgfnyd".
Note however that this chain does not always contain the hash value h; it may so happen that the chain starting at h merges with the chain starting at the starting point at some point after h. For example, we may be given a hash value FB107E70, and when we follow its chain, we get kiebgt:

But FB107E70 is not in the chain starting at "aaaaaa". This is called a false alarm. In this case, we ignore the match and continue to extend the chain of h looking for another match. If the chain of h gets extended to length k with no good matches, then the password was never produced in any of the chains.
The table content does not depend on the hash value to be inverted. It is created once and then repeatedly used for the lookups unmodified. Increasing the length of the chain decreases the size of the table. It also increases the time required to perform lookups, and this is the time-memory trade-off of the rainbow table. In a simple case of one-item chains, the lookup is very fast, but the table is very big. Once chains get longer, the lookup slows down, but the table size goes down.
Simple hash chains have several flaws. Most serious if at any point two chains collide (produce the same value), they will merge and consequently the table will not cover as many passwords despite having paid the same computational cost to generate. Because previous chains are not stored in their entirety, this is impossible to detect efficiently. For example, if the third value in chain 3 matches the second value in chain 7, the two chains will cover almost the same sequence of values, but their final values will not be the same. The hash function H is unlikely to produce collisions as it usually considered an important security feature not to do so, but the reduction function R, because of its need to correctly cover the likely plaintexts, can not be collision resistant.
Other difficulties result from the importance of choosing the correct function for R. Picking R to the identity is little better than a brute force approach. Only when the attacker has a good idea of what the likely plaintexts will be can he choose a function R that makes sure only time and space are used for likely plaintexts not the entire space of possible passwords. In effect R shepherds the results of prior hash calculations back to likely plaintexts but this benefit comes with drawback that R likely won't produce every possible plaintext in the class the attacker wishes to check denying certainty to the attacker that no passwords came from his chosen class. Also it can be difficult to design the function R to match the expected distribution of plaintexts.
Rainbow tables
Rainbow tables effectively solve the problem of collisions with ordinary hash chains by replacing the single reduction function R with a sequence of related reduction functions R1 through Rk. This way, in order for two chains to collide and merge, they must hit the same value on the same iteration. Consequently, the final values in each chain will be identical. A final postprocessing pass can sort the chains in the table and remove any "duplicate" chains that have the same final value as other chains. New chains are then generated to fill out the table. These chains are not collision-free (they may overlap briefly) but they will not merge, drastically reducing the overall number of collisions.Using sequences of reduction functions changes how lookup is done: because the hash value of interest may be found at any location in the chain, it's necessary to generate k different chains. The first chain assumes the hash value is in the last hash position and just applies Rk; the next chain assumes the hash value is in the second-to-last hash position and applies Rk−1, then H, then Rk; and so on until the last chain, which applies all the reduction functions, alternating with H. This creates a new way of producing a false alarm: if we "guess" the position of the hash value wrong, we may needlessly evaluate a chain.
Although rainbow tables have to follow more chains, they make up for this by having fewer tables: simple hash chain tables cannot grow beyond a certain size without rapidly becoming inefficient due to merging chains; to deal with this, they maintain multiple tables, and each lookup must search through each table. Rainbow tables can achieve similar performance with tables that are k times larger, allowing them to perform a factor of k fewer lookups.
Example
We have a hash (re3xes) and we want to find one password that produces that hash.- Starting from the hash ("re3xes"), one computes the last reduction used in the table and checks whether the password appears in the last column of the table (step 1).
- If the test fails (rambo doesn't appear in the table), one computes a chain with the two last reductions (these two reductions are represented at step 2)
- Note: If this new test fails again, one continues with 3 reductions, 4 reductions, etc. until the password is found. If no chain contains the password, then the attack has failed.
- If this test is positive (step 3, linux23 appears at the end of the chain and in the table), the password is retrieved at the beginning of the chain that produces linux23. Here we find passwd at the beginning of the corresponding chain stored in the table.
- At this point (step 4), one generates a chain and compares at each iteration the hash with the target hash. The test is valid and we find the hash re3xes in the chain. The current password (culture) is the one that produced the whole chain: the attack is successful.
Rainbow tables use a refined algorithm with a different reduction function for each "link" in a chain, so that when there is a hash collision in two or more chains the chains will not merge as long as the collision doesn't occur at the same position in each chain. As well as increasing the probability of a correct crack for a given table size, this use of multiple reduction functions approximately doubles the speed of lookups. See the paper cited below for details.
Rainbow tables are specific to the hash function they were created for e.g., MD5
MD5
The MD5 Message-Digest Algorithm is a widely used cryptographic hash function that produces a 128-bit hash value. Specified in RFC 1321, MD5 has been employed in a wide variety of security applications, and is also commonly used to check data integrity...
tables can crack only MD5 hashes. The theory of this technique was first pioneered by Philippe Oechslin as a fast form of time-memory tradeoff
Space-time tradeoff
In computer science, a space–time or time–memory tradeoff is a situation where the memory use can be reduced at the cost of slower program execution...
, which he implemented in the Windows
Microsoft Windows
Microsoft Windows is a series of operating systems produced by Microsoft.Microsoft introduced an operating environment named Windows on November 20, 1985 as an add-on to MS-DOS in response to the growing interest in graphical user interfaces . Microsoft Windows came to dominate the world's personal...
password cracker
Password cracking
Password cracking is the process of recovering passwords from data that has been stored in or transmitted by a computer system. A common approach is to repeatedly try guesses for the password...
Ophcrack
Ophcrack
Ophcrack is a free open source program that cracks Windows passwords by using LM hashes through rainbow tables. The program includes the ability to import the hashes from a variety of formats, including dumping directly from the SAM files of Windows...
. The more powerful RainbowCrack
RainbowCrack
RainbowCrack is a computer program which generates rainbow tables to be used in password cracking. RainbowCrack differs from "conventional" brute force crackers in that it uses large pre-computed tables called rainbow tables to reduce the length of time needed to crack a password drastically...
program was later developed that can generate and use rainbow tables for a variety of character sets and hashing algorithms, including LM hash
LM hash
LM hash, LanMan, or LAN Manager hash was the primary hash that Microsoft LAN Manager and Microsoft Windows versions prior to Windows NT used to store user passwords...
, MD5
MD5
The MD5 Message-Digest Algorithm is a widely used cryptographic hash function that produces a 128-bit hash value. Specified in RFC 1321, MD5 has been employed in a wide variety of security applications, and is also commonly used to check data integrity...
, SHA1, etc..
Defense against rainbow tables
A rainbow table is ineffective against one-way hashes that include saltsSalt (cryptography)
In cryptography, a salt consists of random bits, creating one of the inputs to a one-way function. The other input is usually a password or passphrase. The output of the one-way function can be stored rather than the password, and still be used for authenticating users. The one-way function...
. For example, consider a password hash that is generated using the following function (where "." is the concatenation
Concatenation
In computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
operator):
saltedhash(password) = hash(password.salt)Or
saltedhash(password) = hash(hash(password).salt)The salt value is not secret and may be generated at random and stored with the password hash. A large salt value prevents precomputation attacks, including rainbow tables, by ensuring that each user's password is hashed uniquely. This means that two users with the same password will have different password hashes (assuming different salts are used). In order to succeed, an attacker needs to precompute tables for each possible salt value. The salt must be large enough, otherwise an attacker can make a table for each salt value. For older Unix passwords
Crypt (Unix)
In Unix computing, crypt is the name of both a utility program and a C programming function. Though both are used for encrypting data, they are otherwise essentially unrelated...
which used a 12-bit salt this would require 4096 tables, a significant increase in cost for the attacker, but not impractical with terabyte hard drives. The MD5-crypt and bcrypt methods—used in Linux
Linux
Linux is a Unix-like computer operating system assembled under the model of free and open source software development and distribution. The defining component of any Linux system is the Linux kernel, an operating system kernel first released October 5, 1991 by Linus Torvalds...
, BSD Unixes, and Solaris—have salts of 48 and 128 bits, respectively. These larger salt values make precomputation attacks for almost any length of password infeasible against these systems for the foreseeable future.
Another technique that helps prevent precomputation attacks is key stretching. When stretching is used, the salt, password, and a number of intermediate hash values are run through the underlying hash function multiple times to increase the computation time required to hash each password. For instance, MD5-Crypt uses a 1000 iteration loop that repeatedly feeds the salt, password, and current intermediate hash value back into the underlying MD5 hash function. The user's password hash is the concatenation of the salt value (which is not secret) and the final hash. The extra time is not noticeable to a user because the user only has to wait a fraction of a second each time the user logs in. On the other hand, stretching greatly reduces the effectiveness of a brute-force or precomputation attacks because it reduces the number of computations an attacker can perform in a given time frame. This principle is applied in MD5-Crypt and in bcrypt.
An alternative approach, called key strengthening, extends the key with a random salt, but then (unlike in key stretching) securely deletes the salt. This forces both the attacker and legitimate users to perform a brute-force search for the salt value. Although the paper that introduced key stretching referred to this earlier technique and intentionally chose a different name, the term "key strengthening" is now often (arguably incorrectly) used to refer to key stretching.
Rainbow tables and other precomputation attacks do not work against passwords that contain symbols outside the range presupposed, or that are longer than those precomputed by the attacker. However tables can be generated that take into account common ways in which users attempt to choose more secure passwords, such as adding a number or special character. Because of the sizable investment in computing processing, rainbow tables beyond fourteen places in length are not yet common. So, choosing a password that is longer than fourteen characters may force an attacker to resort to brute-force methods.
Certain intensive efforts focused on LM hash
LM hash
LM hash, LanMan, or LAN Manager hash was the primary hash that Microsoft LAN Manager and Microsoft Windows versions prior to Windows NT used to store user passwords...
, an older hash algorithm used by Microsoft, are publicly available. LM hash is particularly vulnerable because passwords longer than 7 characters are broken into two sections, each of which is hashed separately. Choosing a password that is fifteen characters or longer guarantees that an LM hash will not be generated.
Common uses
Nearly all distributions and variations of UnixUnix
Unix is a multitasking, multi-user computer operating system originally developed in 1969 by a group of AT&T employees at Bell Labs, including Ken Thompson, Dennis Ritchie, Brian Kernighan, Douglas McIlroy, and Joe Ossanna...
, Linux
Linux
Linux is a Unix-like computer operating system assembled under the model of free and open source software development and distribution. The defining component of any Linux system is the Linux kernel, an operating system kernel first released October 5, 1991 by Linus Torvalds...
, and BSD use hashes with salts, though many applications use just a hash (typically MD5
MD5
The MD5 Message-Digest Algorithm is a widely used cryptographic hash function that produces a 128-bit hash value. Specified in RFC 1321, MD5 has been employed in a wide variety of security applications, and is also commonly used to check data integrity...
) with no salt. The Microsoft Windows NT/2000 family uses the LAN Manager
LM hash
LM hash, LanMan, or LAN Manager hash was the primary hash that Microsoft LAN Manager and Microsoft Windows versions prior to Windows NT used to store user passwords...
and NT LAN Manager
NTLM
In a Windows network, NTLM is a suite of Microsoft security protocols that provides authentication, integrity, and confidentiality to users....
hashing method and is also unsalted, which makes it one of the more popularly generated tables.
See also
- A5/1A5/1A5/1 is a stream cipher used to provide over-the-air communication privacy in the GSM cellular telephone standard. It was initially kept secret, but became public knowledge through leaks and reverse engineering. A number of serious weaknesses in the cipher have been identified.-History and...
- Brute force attackBrute force attackIn cryptography, a brute-force attack, or exhaustive key search, is a strategy that can, in theory, be used against any encrypted data. Such an attack might be utilized when it is not possible to take advantage of other weaknesses in an encryption system that would make the task easier...
- Dictionary attackDictionary attackIn cryptanalysis and computer security, a dictionary attack is a technique for defeating a cipher or authentication mechanism by trying to determine its decryption key or passphrase by searching likely possibilities.-Technique:...
- Pollard's kangaroo algorithm
External links
- Project ADIF A general system to distributively invert one-way-functions using time-memory tradeoff
- Project RainbowCrack A rainbow table generator
- Ophcrack page by Philippe Oechslin The original rainbow table research with online demo
- How Rainbow Tables work
- Freerainbowtables.com Free distributed rainbow table generation
- The Shmoo Group The Shmoo Group Rainbow Tables
- Rainbow Tables FAQ (Section 4) In-depth explanation about Rainbow Tables and how they work

