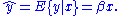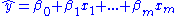Ramsey reset test
Encyclopedia
The Ramsey Regression Equation Specification Error Test (RESET) test (Ramsey, 1969) is a general specification test for the linear regression
model. More specifically, it tests whether non-linear combinations of the estimated values help explain the endogenous
variable. The intuition behind the test is that, if non-linear combinations of the explanatory variables have any power in explaining the endogenous variable, then the model is mis-specified.
The Ramsey test then tests whether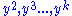
has any power in explaining 
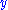. This is executed by estimating the following linear regression
and then testing, by a means of a F-test
whether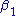
through 
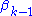are zero. If the null-hypothesis that all regression coefficients of the non-linear terms are zero is rejected, then the model suffers from mis-specification.
For a univariate x the test can also be performed by regressing on the truncated power series of the explanatory variable and using an F-Test for
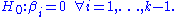
Test rejection implies the same insight as the first version mentioned above.
The F-test compares both regressions, the original one and the Ramsey's auxiliary one, as done with the evaluation of linear restrictions. The original model is the restricted one opposed to the Ramsey's unrestricted model.
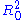is the determination coefficient of the original linear model regression;
is the determination coefficient of the Ramsey's auxiliary regression;
is the sample size;
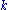is number of parameters in the Ramsey's model.
Furthermore, the linear model
and the model with the non-linear power terms
are sujected to the F-test, similarly as before:
where
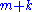is number of parameters in the Ramsey's model, which are 
variables in the Ramsey group (non-linear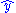 
) plus 
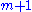the number of parameters in the original model.
The critical (rejection) region is on the right side of the F distribution, thus
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
model. More specifically, it tests whether non-linear combinations of the estimated values help explain the endogenous
Endogenous
Endogenous substances are those that originate from within an organism, tissue, or cell. Endogenous retroviruses are caused by ancient infections of germ cells in humans, mammals and other vertebrates...
variable. The intuition behind the test is that, if non-linear combinations of the explanatory variables have any power in explaining the endogenous variable, then the model is mis-specified.
Technical summary
Consider the model
The Ramsey test then tests whether
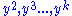has any power in explaining 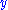. This is executed by estimating the following linear regressionLinear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
-
,
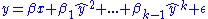and then testing, by a means of a F-test
F-test
An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
whether
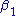through 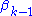are zero. If the null-hypothesis that all regression coefficients of the non-linear terms are zero is rejected, then the model suffers from mis-specification.For a univariate x the test can also be performed by regressing on the truncated power series of the explanatory variable and using an F-Test for
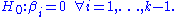
Test rejection implies the same insight as the first version mentioned above.
The F-test compares both regressions, the original one and the Ramsey's auxiliary one, as done with the evaluation of linear restrictions. The original model is the restricted one opposed to the Ramsey's unrestricted model.
-
~ 
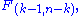where:
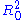is the determination coefficient of the original linear model regression; is the determination coefficient of the Ramsey's auxiliary regression; is the sample size;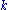 is number of parameters in the Ramsey's model.Furthermore, the linear model
and the model with the non-linear power terms
-
,
are sujected to the F-test, similarly as before:
-
~ 
,
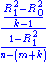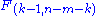where
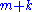is number of parameters in the Ramsey's model, which are variables in the Ramsey group (non-linear 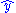) plus 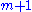the number of parameters in the original model.The critical (rejection) region is on the right side of the F distribution, thus
-
.
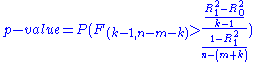