
Random close pack
Encyclopedia
Random close packing is an empirical parameter used to characterize the maximum volume
fraction of solid
objects obtained when they are packed randomly. For example, when a solid container is filled with grain
, shaking the container will reduce the volume taken up by the objects, thus allowing more grain to be added to the container. In other words shaking increases the density of packed objects.
Experiments have shown that the most compact way to pack spheres gives a maximum density of about 64%. Most recent research predicts analytically that the volume fraction filled by the solid objects in random close packing cannot exceed a density limit of 63.4% for (monodisperse
) spherical objects. This is significantly smaller than the maximum theoretical filling fraction of 0.74048 that results from hexagonal close pack (HCP – also known as close-packing
). This discrepancy demonstrates that the "randomness" of RCP is vital to the definition.
decreases. Thus RCP is the packing fraction given by the limit
as the tapping amplitude goes to zero, and the limit as the number of taps goes to infinity
.
candy it is 0.68.
The permeability
of beds of close packed spheres has been extensibility studied because it is one of the basic models of porous media. Multiple formulas have been proposed to express permeability of such a bed a function of bed porosity.
The Carman-Kozeny model predicts that: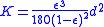
where:
Rumpf and Gupte gave the following equation, which replicates better experimental data:
Usually during shipping, the container will be bumped numerous times, which will increase the packing density.
The message is added to assure the consumer that the container is full on a mass basis, even though the container appears slightly empty.
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
fraction of solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
objects obtained when they are packed randomly. For example, when a solid container is filled with grain
GRAIN
GRAIN is a small international non-profit organisation that works to support small farmers and social movements in their struggles for community-controlled and biodiversity-based food systems. Our support takes the form of independent research and analysis, networking at local, regional and...
, shaking the container will reduce the volume taken up by the objects, thus allowing more grain to be added to the container. In other words shaking increases the density of packed objects.
Experiments have shown that the most compact way to pack spheres gives a maximum density of about 64%. Most recent research predicts analytically that the volume fraction filled by the solid objects in random close packing cannot exceed a density limit of 63.4% for (monodisperse
Monodisperse
A collection of objects are called monodisperse, or monosized, if they have the same size and shape when discussing particles, and the same mass when discussing polymers...
) spherical objects. This is significantly smaller than the maximum theoretical filling fraction of 0.74048 that results from hexagonal close pack (HCP – also known as close-packing
Close-packing
In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement . Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a regular lattice...
). This discrepancy demonstrates that the "randomness" of RCP is vital to the definition.
Definition
Random close packing does not have a precise geometric definition. It is defined statistically, and results are empirical. A container is randomly filled with objects, and then the container is shaken or tapped until the objects do not compact any further, at this point the packing state is RCP. The definition of packing fraction can be given as: "the volume taken by number of particles in a given space of volume". In other words packing fraction defines the packing density. It has been shown that the filling fraction increases logarithmically with the number of taps until the saturation density is reached. Also, the saturation density increases as the tapping amplitudeAmplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
decreases. Thus RCP is the packing fraction given by the limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
as the tapping amplitude goes to zero, and the limit as the number of taps goes to infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
.
Effect of object shape
The particle volume fraction at RCP depends on the objects being packed. If the objects are polydispersed then the volume fraction depends non-trivially on the size-distribution and can be arbitrarily close to 1. Still for (relatively) monodisperse objects the value for RCP depends on the object shape; for spheres it is 0.64, for M&M'sM&M's
M&M's are dragée-like "colorful button-shaped candies" produced by Mars, Incorporated...
candy it is 0.68.
For spheres
| Model | Description | Void fraction Porosity Porosity or void fraction is a measure of the void spaces in a material, and is a fraction of the volume of voids over the total volume, between 0–1, or as a percentage between 0–100%... |
Packing density |
|---|---|---|---|
| Thinnest regular packing | Coordination number Coordination number In chemistry and crystallography, the coordination number of a central atom in a molecule or crystal is the number of its nearest neighbours. This number is determined somewhat differently for molecules and for crystals.... = 6 |
0.4764 | 0.5236 |
| Very loose random packing | E.g., spheres slowly settling | 0.44 | 0.56 |
| Loose random packing | E.g., spheres dropped into bed or packed by hand | 0.40 to 0.41 | 0.59 to 0.60 |
| Poured random packing | Spheres poured into bed | 0.375 to 0.391 | 0.609 to 0.625 |
| Close random packing | E.g., the bed vibrated | 0.359 to 0.375 | 0.625 to 0.641 |
| Thickest regular packing | Coordination number = 12 | 0.2595 | 0.7405 |
The permeability
Permeability (fluid)
Permeability in fluid mechanics and the earth sciences is a measure of the ability of a porous material to allow fluids to pass through it.- Units :...
of beds of close packed spheres has been extensibility studied because it is one of the basic models of porous media. Multiple formulas have been proposed to express permeability of such a bed a function of bed porosity.
The Carman-Kozeny model predicts that:
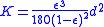
where:
- K – permeability (m2)
-
 – porosity (dimensionless)
– porosity (dimensionless) - d – sphere diameter (m)
Rumpf and Gupte gave the following equation, which replicates better experimental data:

Example
Products containing loose pack items are often labeled with this message: 'Contents May Settle During Shipping'.Usually during shipping, the container will be bumped numerous times, which will increase the packing density.
The message is added to assure the consumer that the container is full on a mass basis, even though the container appears slightly empty.

