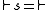Rational consequence relation
Encyclopedia
In mathematical logic
, a rational consequence relation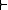
is a logical consequence relation satisfying the properties listed below.
and the so-called Gabbay-Makinson rules:
is intended to carry the meaning theta usually implies phi or phi usually follows from theta. In this sense it is more useful for modeling some everyday situations than a monotone consequence relation because the latter relation models facts in a more strict boolean fashion - something either follows under all circumstances or it does not.
Note that if we also have the information "If a cake contains sugar then it usually contains butter" then we may legally conclude (under CMO) that "If a cake contains sugar and butter then it usually tastes good.". Equally in the absence of a statement such as "If a cake contains sugar then usually it contains no soap" then we may legally conclude from RMO that "If the cake contains sugar and soap then it usually tastes good."
If this latter conclusion seems ridiculous to you then it is likely that you are subconsciously asserting your own preconceived knowledge about cakes when evaluating the validity of the statement. That is, from your experience you know that cakes which contain soap are likely to taste bad so you add to the system your own knowledge such as "Cakes which contain sugar do not usually contain soap.", even though this knowledge is absent from it. If the conclusion seems silly to you then you might consider replacing the word soap with the word eggs to see if it changes your feelings.
We may consider it reasonable to conclude:
This would not be a valid conclusion under a monotonic deduction system (omitting of course the word 'usually'), since the third sentence would contradict the first two. In contrast the conclusion follows immediately using the Gabbay-Makinson rules: applying the rule CMO to the last two sentences yields the result.
be a finite language. An atom is a formula of the form 
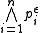(where 
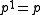and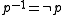 
). Notice that there is a unique valuation which makes any given atom true (and conversely each valuation satisfies precisely one atom). Thus an atom can be used to represent a preference about what we believe ought to be true.
Let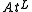
be the set of all atoms in L. For 
SL, define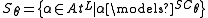 
.
Let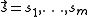
be a sequence of subsets of 
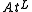. For 
, 
in SL, let the relation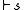 
be such that 
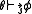if one of the following holds:
Then the relation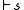
is a rational consequence relation. This may easily be verified by checking directly that it satisfies the GM-conditions.
The idea behind the sequence of atom sets is that the earlier sets account for the most likely situations such as "young people are usually law abiding" whereas the later sets account for the less likely situations such as "young joyriders are usually not law abiding".
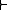there is a sequence 
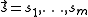of subsets of 
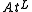such that the associated rcr 
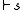is the same relation: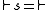 
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a rational consequence relation
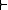is a logical consequence relation satisfying the properties listed below.Properties
A rational consequence relation satisfies:-
- REF : ReflexivityReflexive relationIn mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
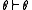
- REF : Reflexivity
and the so-called Gabbay-Makinson rules:
-
- LLE : Left Logical Equivalence
- RWE : Right-hand weakening
- CMO : Cautious monotonicity
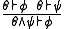
- DIS : Logical or (ie disjunction) on left hand side
- AND : Logical and on right hand side
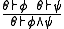
- RMO : Rational monotonicity
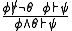
- LLE : Left Logical Equivalence
Uses
The rational consequence relation is non-monotonic, and the relation is intended to carry the meaning theta usually implies phi or phi usually follows from theta. In this sense it is more useful for modeling some everyday situations than a monotone consequence relation because the latter relation models facts in a more strict boolean fashion - something either follows under all circumstances or it does not.Example
The statement "If a cake contains sugar then it tastes good" implies under a monotone consequence relation the statement "If a cake contains sugar and soap then it tastes good." Clearly this doesn't match our own understanding of cakes. By asserting "If a cake contains sugar then it usually tastes good" a rational consequence relation allows for a more realistic model of the real world, and certainly it does not automatically follow that "If a cake contains sugar and soap then it usually tastes good."Note that if we also have the information "If a cake contains sugar then it usually contains butter" then we may legally conclude (under CMO) that "If a cake contains sugar and butter then it usually tastes good.". Equally in the absence of a statement such as "If a cake contains sugar then usually it contains no soap" then we may legally conclude from RMO that "If the cake contains sugar and soap then it usually tastes good."
If this latter conclusion seems ridiculous to you then it is likely that you are subconsciously asserting your own preconceived knowledge about cakes when evaluating the validity of the statement. That is, from your experience you know that cakes which contain soap are likely to taste bad so you add to the system your own knowledge such as "Cakes which contain sugar do not usually contain soap.", even though this knowledge is absent from it. If the conclusion seems silly to you then you might consider replacing the word soap with the word eggs to see if it changes your feelings.
Example
Consider the sentences:- Young people are usually happy
- Drug abusers are usually not happy
- Drug abusers are usually young
We may consider it reasonable to conclude:
- Young drug abusers are usually not happy
This would not be a valid conclusion under a monotonic deduction system (omitting of course the word 'usually'), since the third sentence would contradict the first two. In contrast the conclusion follows immediately using the Gabbay-Makinson rules: applying the rule CMO to the last two sentences yields the result.
Consequences
The following consequences follow from the above rules:-
- MP : Modus ponensModus ponensIn classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
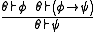
- MP is proved via the rules AND and RWE.
- MP : Modus ponens
-
- CON : Conditionalisation
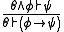
- CON : Conditionalisation
-
- CC : Cautious Cut
- The notion of Cautious Cut simply encapsulates the operation of conditionalisation, followed by MP. It may seem redundant in this sense, but it is often used in proofs so it is useful to have a name for it to act as a shortcut.
- CC : Cautious Cut
-
- SCL : Supraclassity
- SCL is proved trivially via REF and RWE.
- SCL : Supraclassity
Rational consequence relations via atom preferences
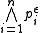Let be a finite language. An atom is a formula of the form (where 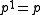and 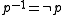). Notice that there is a unique valuation which makes any given atom true (and conversely each valuation satisfies precisely one atom). Thus an atom can be used to represent a preference about what we believe ought to be true.Let
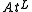be the set of all atoms in L. For 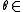SL, define 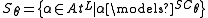.Let
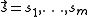be a sequence of subsets of 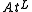. For 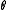, 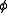in SL, let the relation 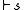be such that 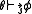if one of the following holds:
for each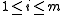 
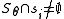for some 
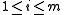and for the least such i, 
.
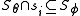Then the relation
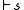is a rational consequence relation. This may easily be verified by checking directly that it satisfies the GM-conditions.The idea behind the sequence of atom sets is that the earlier sets account for the most likely situations such as "young people are usually law abiding" whereas the later sets account for the less likely situations such as "young joyriders are usually not law abiding".
The representation theorem
It can be proven that any rational consequence relation on a finite language is representable via a sequence of atom preferences above. That is, for any such rational consequence relation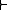 there is a sequence 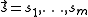of subsets of 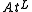such that the associated rcr 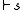is the same relation: