
Rational dependence
Encyclopedia
In mathematics, a collection of real number
s is rationally independent if none of them can be written as a linear combination of the other numbers in the collection with rational
coefficients. A collection of numbers which is not rationally independent is called rationally dependent. For instance we have the following example.
s ω1, ω2, ... , ωn are said to be rationally dependent if there exist integers k1, k2, ... , kn not all zero, such that

If such integers do not exist, then the vectors are said to be rationally independent. This condition can be reformulated as follows: ω1, ω2, ... , ωn are rationally independent if whenever k1, k2, ... , kn are integers such that
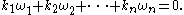
we have ki = 0 for i = 1, 2, ..., n, i.e. only the trivial solution
exists on the integers. Note that if we consider the reals as a vector space
over the rationals, this is just the usual definition of linear independence
.
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is rationally independent if none of them can be written as a linear combination of the other numbers in the collection with rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
coefficients. A collection of numbers which is not rationally independent is called rationally dependent. For instance we have the following example.

Formal definition
The real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s ω1, ω2, ... , ωn are said to be rationally dependent if there exist integers k1, k2, ... , kn not all zero, such that

If such integers do not exist, then the vectors are said to be rationally independent. This condition can be reformulated as follows: ω1, ω2, ... , ωn are rationally independent if whenever k1, k2, ... , kn are integers such that
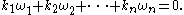
we have ki = 0 for i = 1, 2, ..., n, i.e. only the trivial solution
Trivial (mathematics)
In mathematics, the adjective trivial is frequently used for objects that have a very simple structure...
exists on the integers. Note that if we consider the reals as a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the rationals, this is just the usual definition of linear independence
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
.

