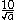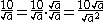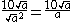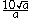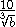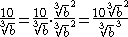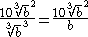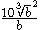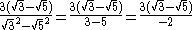Rationalisation (mathematics)
Encyclopedia
In elementary algebra
, root rationalisation is a process by which surds
in the denominator of an irrational fraction are eliminated.
These surds may be monomial
s or binomial
s involving square root
s, in simple examples. There are wide extensions to the technique.
Example 1:
To rationalise this kind of monomial
, bring in the factor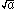 :
:
The square root
disappears from the denominator, because it is squared:
This gives the result, after simplification:
Example 2:
To rationalise this radical, bring in the factor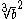 :
:
The cube root disappears from the denominator, because it is cubed:
This gives the result, after simplification:
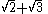
Rationalisation can be achieved by multiplying by the Conjugate
:
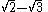
and applying the difference of two squares
identity, which here will yield −1. To get this result, the entire fraction should be multiplied by
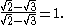
This technique works much more generally. It can easily be adapted to remove one square root at a time, i.e. to rationalise
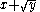
by multiplication by
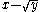
Example:
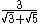
The fraction must be multiplied by a quotient containing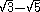 .
.
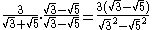
Now, we can proceed to remove the square roots in the denominator:
s and algebraic function
s (as an application of norm form
s). For example, to rationalise a cube root, two linear factors involving cube roots of unity should be used, or equivalently a quadratic factor.
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
, root rationalisation is a process by which surds
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
in the denominator of an irrational fraction are eliminated.
These surds may be monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s or binomial
Binomial
In algebra, a binomial is a polynomial with two terms —the sum of two monomials—often bound by parenthesis or brackets when operated upon...
s involving square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s, in simple examples. There are wide extensions to the technique.
Rationalisation of a monomial square root and cube root
For the fundamental technique, the numerator and denominator must be multiplied, but by the same factor.Example 1:
To rationalise this kind of monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
, bring in the factor
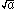 :
:The square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
disappears from the denominator, because it is squared:
This gives the result, after simplification:
Example 2:
To rationalise this radical, bring in the factor
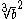 :
:The cube root disappears from the denominator, because it is cubed:
This gives the result, after simplification:
Dealing with more square roots
For a denominator that is: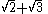
Rationalisation can be achieved by multiplying by the Conjugate
Conjugate (algebra)
In algebra, a conjugate of an element in a quadratic extension field of a field K is its image under the unique non-identity automorphism of the extended field that fixes K. If the extension is generated by a square root of an element...
:
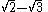
and applying the difference of two squares
Difference of two squares
In mathematics, the difference of two squares, or the difference of perfect squares, is when a number is squared, or multiplied by itself, and is then subtracted from another squared number...
identity, which here will yield −1. To get this result, the entire fraction should be multiplied by
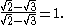
This technique works much more generally. It can easily be adapted to remove one square root at a time, i.e. to rationalise
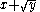
by multiplication by
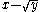
Example:
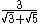
The fraction must be multiplied by a quotient containing
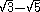 .
.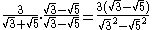
Now, we can proceed to remove the square roots in the denominator:
Generalisations
Rationalisation can be extended to all algebraic numberAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s and algebraic function
Algebraic function
In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
s (as an application of norm form
Norm form
In mathematics, a norm form is a homogeneous form in n variables constructed from the field norm of a field extension L/K of degree n...
s). For example, to rationalise a cube root, two linear factors involving cube roots of unity should be used, or equivalently a quadratic factor.