
Real gas
Encyclopedia
Real gases – as opposed to a perfect or ideal gas
– exhibit properties that cannot be explained entirely using the ideal gas law
. To understand the behaviour of real gases, the following must be taken into account:
For most applications, such a detailed analysis is unnecessary, and the ideal gas approximation can be used with reasonable accuracy. On the other hand, real-gas models have to be used near the condensation
point of gases, near critical point
s, at very high pressures, and in other less usual cases.
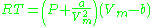
Where P is the pressure, T is the temperature, R the ideal gas constant, and Vm the molar volume. a and b are parameters that are determined empirically for each gas, but are sometimes estimated from their critical temperature (Tc) and critical pressure (Pc) using these relations:
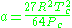
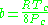
is another two-parameters equation that is used to model real gases. It is almost always more accurate than the van der Waals equation
, and often more accurate than some equations with more than two parameters. The equation is
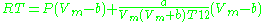
where a and b two empirical parameters that are not the same parameters as in the van der Waals equation. These parameters can be determined:
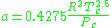
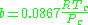
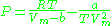
but the modified version is somewhat more accurate
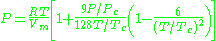
 .
.
) is a very simple three-parameter equation used to model gases.
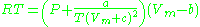
where
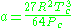
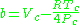
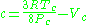
where Vc is critical volume.
of statistical mechanics.
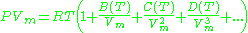
or alternatively
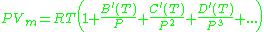
where A, B, C, A′, B′, and C′ are temperature dependent constants.
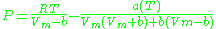
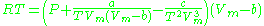
where
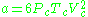
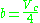
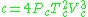 .
.
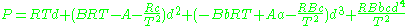
where d is the molal density and a, b, c, A, and B are empirical parameters.
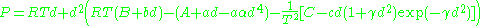
where d is the molal density and where a, b, c, A, B, C, α, and γ are empirical constants.
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
– exhibit properties that cannot be explained entirely using the ideal gas law
Ideal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
. To understand the behaviour of real gases, the following must be taken into account:
- compressibility effects;
- variable specific heat capacity;
- van der Waals forceVan der Waals forceIn physical chemistry, the van der Waals force , named after Dutch scientist Johannes Diderik van der Waals, is the sum of the attractive or repulsive forces between molecules other than those due to covalent bonds or to the electrostatic interaction of ions with one another or with neutral...
s; - non-equilibrium thermodynamic effects;
- issues with molecular dissociation and elementary reactions with variable composition.
For most applications, such a detailed analysis is unnecessary, and the ideal gas approximation can be used with reasonable accuracy. On the other hand, real-gas models have to be used near the condensation
Condensation
Condensation is the change of the physical state of matter from gaseous phase into liquid phase, and is the reverse of vaporization. When the transition happens from the gaseous phase into the solid phase directly, the change is called deposition....
point of gases, near critical point
Critical point (thermodynamics)
In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions at which a phase boundary ceases to exist...
s, at very high pressures, and in other less usual cases.
Models
van der Waals model
Real gases are often modeled by taking into account their molar weight and molar volume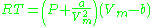
Where P is the pressure, T is the temperature, R the ideal gas constant, and Vm the molar volume. a and b are parameters that are determined empirically for each gas, but are sometimes estimated from their critical temperature (Tc) and critical pressure (Pc) using these relations:
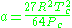
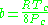
Redlich–Kwong model
The Redlich–Kwong equationRedlich–Kwong equation of state
In physics and thermodynamics, the Redlich–Kwong equation of state is an equation that is derived from the van der Waals equation. It is generally more accurate than the van der Waals equation and the ideal gas equation, but not used as frequently because the increased difficulty in its derivatives...
is another two-parameters equation that is used to model real gases. It is almost always more accurate than the van der Waals equation
Van der Waals equation
The van der Waals equation is an equation of state for a fluid composed of particles that have a non-zero volume and a pairwise attractive inter-particle force It was derived by Johannes Diderik van der Waals in 1873, who received the Nobel prize in 1910 for "his work on the equation of state for...
, and often more accurate than some equations with more than two parameters. The equation is
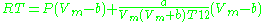
where a and b two empirical parameters that are not the same parameters as in the van der Waals equation. These parameters can be determined:
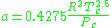
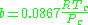
Berthelot and modified Berthelot model
The Berthelot equation (named after D. Berthelot is very rarely used,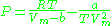
but the modified version is somewhat more accurate
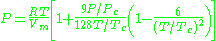
Dieterici model
This model (named after C. Dieterici) fell out of usage in recent years .
.Clausius model
The Clausius equation (named after Rudolf ClausiusRudolf Clausius
Rudolf Julius Emanuel Clausius , was a German physicist and mathematician and is considered one of the central founders of the science of thermodynamics. By his restatement of Sadi Carnot's principle known as the Carnot cycle, he put the theory of heat on a truer and sounder basis...
) is a very simple three-parameter equation used to model gases.
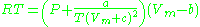
where
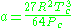
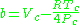
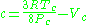
where Vc is critical volume.
Virial model
The Virial equation derives from a perturbative treatmentPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
of statistical mechanics.
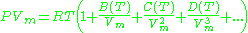
or alternatively
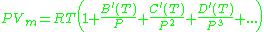
where A, B, C, A′, B′, and C′ are temperature dependent constants.
Peng–Robinson model
This two parameter equation (named after D.-Y. Peng and D. B. Robinson) has the interesting property being useful in modeling some liquids as well as real gases.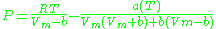
Wohl model
The Wohl equation (named after A. Wohl) is formulated in terms of critical values, making it useful when real gas constants are not available.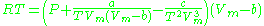
where
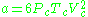
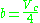
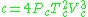 .
.Beattie–Bridgeman model
The Beattie–Bridgeman equation (named after James A. Beattie and Oscar C. Bridgeman)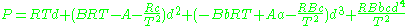
where d is the molal density and a, b, c, A, and B are empirical parameters.
Benedict–Webb–Rubin model
The BWR equation, sometimes referred to as the BWRS equation,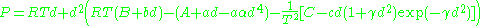
where d is the molal density and where a, b, c, A, B, C, α, and γ are empirical constants.
See also
- Gas lawsGas lawsThe early gas laws were developed at the end of the 18th century, when scientists began to realize that relationships between the pressure, volume and temperature of a sample of gas could be obtained which would hold for all gases...
- Ideal gas lawIdeal gas lawThe ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
by BoyleBoyle's lawBoyle's law is one of many gas laws and a special case of the ideal gas law. Boyle's law describes the inversely proportional relationship between the absolute pressure and volume of a gas, if the temperature is kept constant within a closed system...
& Gay-LussacGay-Lussac's lawThe expression Gay-Lussac's law is used for each of the two relationships named after the French chemist Joseph Louis Gay-Lussac and which concern the properties of gases, though it is more usually applied to his law of combining volumes, the first listed here... - Compressibility factorCompressibility factorThe compressibility factor , also known as the compression factor, is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behavior. In general, deviation from ideal behavior becomes more significant the closer a gas is to a phase change, the lower the...
- Equation of stateEquation of stateIn physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...

