In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, in the field of topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

, a topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

 is said to be realcompact if it is completely regular Hausdorff and every point of its Stone-Cech compactification is real (meaning that the quotient field at that point of the ring of real functions is the reals). Realcompact spaces have also been called Q-spaces, saturated spaces, functionally complete spaces, real-complete spaces, and Hewitt-Nachbin spaces. Realcompact spaces were introduced by .

Properties

• A space is realcompact if and only if it can be embedded homeomorphically as a closed subset in some (not necessarily finite) Cartesian power of the reals, with the product topology. Moreover, a (Hausdorff) space is realcompact if and only if it has the uniform topology and is complete for the uniform structure generated by the continuous real-valued functions (Gillman, Jerison, p. 226).

• For example Lindelöf space
  Lindelöf space
  In mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
  
  s are realcompact; in particular all subsets of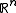 are realcompact.

• The (Hewitt) realcompactification υX of a topological space X consists of the real points of its Stone-Cech compactification βX. A topological space X is realcompact if and only if it coincides with its Hewitt realcompactification.

• Write C(X) for the ring of continuous functions on a topological space X. If Y is a real compact space, then ring homomorphisms from C(Y) to C(X) correspond to continuous maps from X to Y. In particular the category of realcompact spaces is dual to the category of rings of the form C(X).

• In order that a Hausdorff space
  Hausdorff space
  In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
  
   X is compact it is necessary and sufficient that X is realcompact and pseudocompact (see Engelking, p. 153).

See also

• Compact space
  Compact space
  In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
  
  
• Paracompact space
  Paracompact space
  In mathematics, a paracompact space is a topological space in which every open cover admits a locally finite open refinement. Paracompact spaces are sometimes also required to be Hausdorff. Paracompact spaces were introduced by ....
  
  
• Normal space
  Normal space
  In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
  
  
• Pseudocompact space
  Pseudocompact space
  In mathematics, in the field of topology, a topological space is said to be pseudocompact if its image under any continuous function to R is bounded.-Properties related to pseudocompactness:...
  
  
• Tychonoff space
  Tychonoff space
  In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....