Recurrent point
Encyclopedia
In mathematics
, a recurrent point for function f is a point that is in the limit set
of the iterated function
f. Any neighborhood containing the recurrent point will also contain (a countable number of) iterates of it as well.
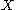be a Hausdorff space
and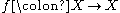
a function. A point 
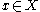is said to be recurrent (for 
) if 
, i.e. if 
belongs to its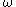 
-limit set
. This means that for each neighborhood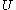
of 
there exists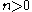 
such that 
.
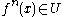The closure of the set of recurrent points of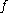
is often denoted 
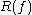and is called the recurrent set of 
.
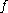Every recurrent point is a nonwandering point, hence if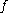
is a homeomorphism
and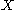
is compact, then 
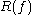is an invariant subset of the non-wandering set of 
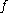(and may be a proper subset).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a recurrent point for function f is a point that is in the limit set
Limit set
In mathematics, especially in the study of dynamical systems, a limit set is the state a dynamical system reaches after an infinite amount of time has passed, by either going forward or backwards in time...
of the iterated function
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
f. Any neighborhood containing the recurrent point will also contain (a countable number of) iterates of it as well.
Definition
Let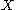 be a Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
and
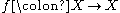a function. A point 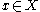is said to be recurrent (for ) if , i.e. if belongs to its 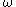-limit setLimit set
In mathematics, especially in the study of dynamical systems, a limit set is the state a dynamical system reaches after an infinite amount of time has passed, by either going forward or backwards in time...
. This means that for each neighborhood
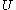of there exists 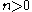such that 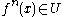.The closure of the set of recurrent points of
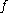is often denoted 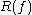and is called the recurrent set of 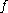.Every recurrent point is a nonwandering point, hence if
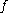is a homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
and
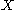is compact, then 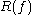is an invariant subset of the non-wandering set of 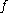(and may be a proper subset).