
Reflexive closure
Encyclopedia
In mathematics
, the reflexive closure of a binary relation
R on a set X is the smallest reflexive relation
on X that contains R.
For example, if X is a set of distinct numbers and x R y means "x is less than y", then the reflexive closure of R is the relation "x is less than or equal to y".
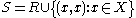
In words, the reflexive closure of R is the union of R with the identity relation on X.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the reflexive closure of a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
R on a set X is the smallest reflexive relation
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
on X that contains R.
For example, if X is a set of distinct numbers and x R y means "x is less than y", then the reflexive closure of R is the relation "x is less than or equal to y".
Definition
The reflexive closure S of a relation R on a set X is given by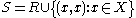
In words, the reflexive closure of R is the union of R with the identity relation on X.

