Regressive discrete fourier series
Encyclopedia
In applied mathematics, the regressive discrete Fourier series (RDFS) is a generalization of the discrete Fourier transform
where the Fourier series
coefficients are computed in a least squares
sense and the period is arbitrary, i.e., not necessarily equal to the length of the data. It was first proposed by Arruda (1992a,1992b). It can be used to smooth data in one or more dimensions and to compute derivatives from the smoothed curve, surface
, or hypersurface
.
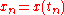, one can write the algebraic expression:
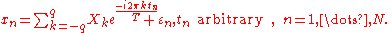
Typically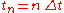
, but this is not necessary.
The above equation can be written in matrix form as
The least squares
solution of the above linear system of equations can be written as:
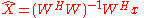
and the smoothed signal is obtained from:
The first derivative of the smoothed signal
can be obtained from:
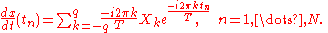
one can write the algebraic expression:
The above equation can be written in matrix form for a rectangular grid. For the equally spaced sampling case :
we have:
The least squares
solution may be shown to be:
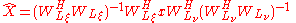
and the smoothed bidimensional surface is given by:
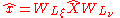
Differentiation with respect to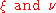
can be easily implemented analogously to the one-dimensional case (Arruda, 1992b).
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
where the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
coefficients are computed in a least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
sense and the period is arbitrary, i.e., not necessarily equal to the length of the data. It was first proposed by Arruda (1992a,1992b). It can be used to smooth data in one or more dimensions and to compute derivatives from the smoothed curve, surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
, or hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
.
One-dimensional regressive discrete Fourier series (RDFS)
The one-dimensional RDFS proposed by Arruda (1992a) can be formulated in a very straightforward way. Given a sampled data vector (signal)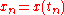, one can write the algebraic expression: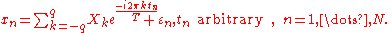Typically
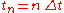, but this is not necessary.The above equation can be written in matrix form as
The least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
solution of the above linear system of equations can be written as:
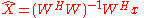
and the smoothed signal is obtained from:
The first derivative of the smoothed signal
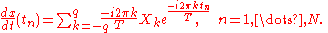
can be obtained from:Two-dimensional regressive discrete Fourier series (RDFS)
The two-dimensional, or bidimensional RDFS proposed by Arruda (1992b) can also be formulated in a straightforward way. Here the equally spaced data case will be treated for the sake of simplicity. The general non-equally-spaced and arbitrary grid cases are given in the reference (Arruda,1992b). Given a sampled data matrix (bi dimensional signal) one can write the algebraic expression:The above equation can be written in matrix form for a rectangular grid. For the equally spaced sampling case :
we have:The least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
solution may be shown to be:
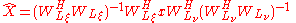
and the smoothed bidimensional surface is given by:
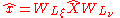
Differentiation with respect to
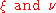can be easily implemented analogously to the one-dimensional case (Arruda, 1992b).Current applications
- Spatially dense data condensation applications: Arruda, J.R.F. [1993] applied the RDFS to condense spatially dense spatial measurements made with a laser Doppler vibrometerLaser Doppler VibrometerA laser Doppler vibrometer is a scientific instrument that is used to make non-contact vibration measurements of a surface. The laser beam from the LDV is directed at the surface of interest, and the vibration amplitude and frequency are extracted from the Doppler shift of the laser beam...
prior to applying modal analysisModal analysisModal analysis is the study of the dynamic properties of structures under vibrational excitation.Modal analysis is the field of measuring and analysing the dynamic response of structures and or fluids when excited by an input...
parameter estimation methods. More recently, Vanherzeele et al. (2006,2008a) proposed a generalized and an optimized RDFS for the same kind of application. A review of optical measurement processing using the RDFS was published by Vanherzeele et al. (2009).
- Spatial derivative applications: Batista et al. [2008b] applied RDFS to obtain spatial derivatives of bi dimensional measured vibration data to identify material properties from transverse modes of rectangular plates.
- SHM applications: Vanherzeele et al. [2009] applied a generalized version of the RDFS to tomographyTomographyTomography refers to imaging by sections or sectioning, through the use of any kind of penetrating wave. A device used in tomography is called a tomograph, while the image produced is a tomogram. The method is used in radiology, archaeology, biology, geophysics, oceanography, materials science,...
reconstruction.