Regret (decision theory)
Encyclopedia
Regret is defined as the difference between the actual payoff and the payoff that would have been obtained if a different course of action had been chosen. This is also called difference regret. Furthermore, the ratio regret is the ratio between the actual payoff and the best one.
regret approach is to minimize the worst-case regret. The aim of this is to perform as closely as possible to the optimal course. Since the minimax criterion applied here is to the regret (difference or ratio of the payoffs) rather than to the payoff itself, it is not as pessimistic as the ordinary minimax approach. Similar approaches have been used in a variety of areas such as:
One benefit of minimax (as opposed to expected regret) is that it is independent of the probabilities of the various outcomes: thus if regret can be accurately computed, one can reliably use minimax regret. However, probabilities of outcomes are hard to estimate.
This differs from the standard minimax approach in that it uses differences or ratios between outcomes, and thus requires interval or ratio measurements, as well as ordinal measurements (ranking), as in standard minimax.
The crude maximin choice based on returns would be to invest in the money market, ensuring a return of at least 1. However, if interest rates fell then the regret associated with this choice would be large. This would be −11, which is the difference between the 1 received and the 12 which could have been received if the outturn had been known in advance. A mixed portfolio of about 11.1% in stocks and 88.9% in the money market would have ensured a return of at least 2.22; but, if interest rates fell, there would be a regret of about −9.78.
The regret table for this example, constructed by subtracting best returns from actual returns, is as follows:
Therefore, using a minimax choice based on regret, the best course would be to invest in bonds, ensuring a regret of no worse than −5. A mixed investment portfolio would do even better: 61.1% invested in stocks, and 38.9% in the money market would produce a regret no worse than about −4.28.
, it generalizes the minimax regret approach. Choice is modelled as the minimising of a function of the regret vector, defined as the difference between the outcome yielded by a given choice and the best outcome that could have been achieved in that state of nature.
. The regret is the difference between the mean-squared error (MSE) of the linear estimator that doesn't know the parameter
, and the mean-squared error (MSE) of the linear estimator that knows 
. Also, since the estimator is restricted to be linear, the zero MSE cannot be achieved in the latter case.
Consider the problem of estimating the unknown deterministic parameter vector
from the noisy measurements in the linear model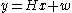
where
is a known 
matrix with full column rank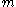 
, and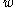 
is a zero mean random vector with covariance matrix 
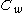, which models the noise.
Let
be a linear estimate of
from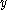 
, where 
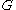is some 
matrix. The MSE of this estimator is given by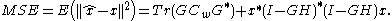
Since the MSE depends explicitly on
it cannot be minimized directly. Instead, the concept of regret can be used in order to define a linear estimator with good MSE performance. To define the regret here, consider a linear estimator that knows the value of the parameter 
, i.e. the matrix 
can explicitly depend on 
:
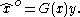
The MSE of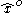
is
To find the optimal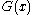
, it is differentated with respect to 
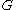and equated to 0 getting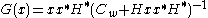
and using the Matrix Inversion Lemma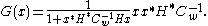
Substituting this
back into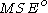 
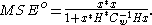
This is the smallest MSE achievable with a linear estimate that knows
. In practice this MSE cannot be achieved, but it serves as a bound on the optimal MSE. The regret is defined by
The minimax regret approach here is to minimize the worst-case regret as defined above. This will allow a performance as close as possible to the best achievable performance in the worst case of the parameter
. Although this problem appears difficult, it can be formulated as a convex optimization problem and solved definitely. For details of this see Eldar, Tal and Nemirovski (2004). Similar ideas can be used when 
is random with uncertainty in the covariance matrix
. For this see Eldar and Merhav (2004), and Eldar and Merhav (2005).
Minimax regret
The minimaxMinimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
regret approach is to minimize the worst-case regret. The aim of this is to perform as closely as possible to the optimal course. Since the minimax criterion applied here is to the regret (difference or ratio of the payoffs) rather than to the payoff itself, it is not as pessimistic as the ordinary minimax approach. Similar approaches have been used in a variety of areas such as:
- Hypothesis testing
- PredictionPredictionA prediction or forecast is a statement about the way things will happen in the future, often but not always based on experience or knowledge...
- EconomicsEconomicsEconomics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
One benefit of minimax (as opposed to expected regret) is that it is independent of the probabilities of the various outcomes: thus if regret can be accurately computed, one can reliably use minimax regret. However, probabilities of outcomes are hard to estimate.
This differs from the standard minimax approach in that it uses differences or ratios between outcomes, and thus requires interval or ratio measurements, as well as ordinal measurements (ranking), as in standard minimax.
Maximin example
Suppose an investor has to choose between investing in stocks, bonds or the money market, and the total return depends on what happens to interest rates. The following table shows some possible returns:| Return | Interest rates rise | Static rates | Interest rates fall | Worst return |
|---|---|---|---|---|
| Stocks | −4 | 4 | 12 | −4 |
| Bonds | −2 | 3 | 8 | −2 |
| Money market | 3 | 2 | 1 | 1 |
| Best return | 3 | 4 | 12 |
The crude maximin choice based on returns would be to invest in the money market, ensuring a return of at least 1. However, if interest rates fell then the regret associated with this choice would be large. This would be −11, which is the difference between the 1 received and the 12 which could have been received if the outturn had been known in advance. A mixed portfolio of about 11.1% in stocks and 88.9% in the money market would have ensured a return of at least 2.22; but, if interest rates fell, there would be a regret of about −9.78.
The regret table for this example, constructed by subtracting best returns from actual returns, is as follows:
| Regret | Interest rates rise | Static rates | Interest rates fall | Worst regret |
|---|---|---|---|---|
| Stocks | −7 | 0 | 0 | −7 |
| Bonds | −5 | −1 | −4 | −5 |
| Money market | 0 | −2 | −11 | −11 |
Therefore, using a minimax choice based on regret, the best course would be to invest in bonds, ensuring a regret of no worse than −5. A mixed investment portfolio would do even better: 61.1% invested in stocks, and 38.9% in the money market would produce a regret no worse than about −4.28.
Regret theory
Regret theory is a model of choice under uncertainty. Developed by Graham Loomes and Robert SugdenRobert Sugden (economist)
Robert Sugden is an English author in the area of cognitive and behavioural economics. Professor Sugden’s research combines game theory with moral and political philosophy...
, it generalizes the minimax regret approach. Choice is modelled as the minimising of a function of the regret vector, defined as the difference between the outcome yielded by a given choice and the best outcome that could have been achieved in that state of nature.
Example: Linear estimation setting
What follows is an illustration of how the concept of regret can be used to design a linear estimatorEstimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
. The regret is the difference between the mean-squared error (MSE) of the linear estimator that doesn't know the parameter
, and the mean-squared error (MSE) of the linear estimator that knows . Also, since the estimator is restricted to be linear, the zero MSE cannot be achieved in the latter case.Consider the problem of estimating the unknown deterministic parameter vector
from the noisy measurements in the linear model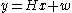where
is a known matrix with full column rank 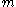, and 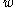is a zero mean random vector with covariance matrix 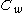, which models the noise.Let
be a linear estimate of
from 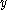, where 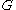is some matrix. The MSE of this estimator is given by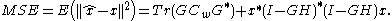Since the MSE depends explicitly on
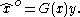
it cannot be minimized directly. Instead, the concept of regret can be used in order to define a linear estimator with good MSE performance. To define the regret here, consider a linear estimator that knows the value of the parameter , i.e. the matrix can explicitly depend on :The MSE of
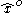isTo find the optimal
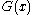, it is differentated with respect to 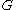and equated to 0 getting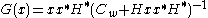and using the Matrix Inversion Lemma
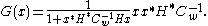
Substituting this
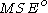
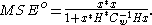
back into This is the smallest MSE achievable with a linear estimate that knows
. In practice this MSE cannot be achieved, but it serves as a bound on the optimal MSE. The regret is defined byThe minimax regret approach here is to minimize the worst-case regret as defined above. This will allow a performance as close as possible to the best achievable performance in the worst case of the parameter
. Although this problem appears difficult, it can be formulated as a convex optimization problem and solved definitely. For details of this see Eldar, Tal and Nemirovski (2004). Similar ideas can be used when is random with uncertainty in the covariance matrixCovariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
. For this see Eldar and Merhav (2004), and Eldar and Merhav (2005).
See also
- Decision theoryDecision theoryDecision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
- Info-gap decision theoryInfo-gap decision theoryInfo-gap decision theory is a non-probabilistic decision theory that seeks to optimize robustness to failure – or opportuneness for windfall – under severe uncertainty, in particular applying sensitivity analysis of the stability radius type to perturbations in the value of a given estimate of the...
- Loss functionLoss functionIn statistics and decision theory a loss function is a function that maps an event onto a real number intuitively representing some "cost" associated with the event. Typically it is used for parameter estimation, and the event in question is some function of the difference between estimated and...
- MinimaxMinimaxMinimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
- Wald's maximin modelWald's maximin modelIn decision theory and game theory, Wald's maximin model is a non-probabilistic decision-making model according to which decisions are ranked on the basis of their worst-case outcomes. That is, the best decision is one whose worst outcome is at least as good as the worst outcome of any other...