
Regular ideal
Encyclopedia
In mathematics, especially ring theory
, a right ideal
 in a non-unital ring A is said to be regular (or modular) if there exists an element e in A such that
in a non-unital ring A is said to be regular (or modular) if there exists an element e in A such that  for every
for every  . In particular, a two-sided ideal
. In particular, a two-sided ideal 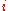 is regular if and only if
is regular if and only if 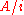 is unital. In a unital ring, every ideal is regular and so the notion is relevant only for non-unital rings such as Banach algebra
is unital. In a unital ring, every ideal is regular and so the notion is relevant only for non-unital rings such as Banach algebra
s. Note that if e is in I, then .
.
The notion of regular ideals permits the generalization of various characterizations of ideals in a unital ring to non-unital settings. In a non-unital ring,
Examples
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, a right ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
 in a non-unital ring A is said to be regular (or modular) if there exists an element e in A such that
in a non-unital ring A is said to be regular (or modular) if there exists an element e in A such that  for every
for every  . In particular, a two-sided ideal
. In particular, a two-sided ideal 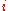 is regular if and only if
is regular if and only if 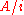 is unital. In a unital ring, every ideal is regular and so the notion is relevant only for non-unital rings such as Banach algebra
is unital. In a unital ring, every ideal is regular and so the notion is relevant only for non-unital rings such as Banach algebraBanach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
s. Note that if e is in I, then
 .
.The notion of regular ideals permits the generalization of various characterizations of ideals in a unital ring to non-unital settings. In a non-unital ring,
- Every proper regular right ideal is contained in a maximal right ideal (a maximal ideal is always regular).
- The Jacobson radicalJacobson radicalIn mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
is the intersection of all maximal regular right (or left) ideals.
Examples
- In the non-unital ring of even integers, (6) is regular (
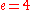 ) while (4) is not.
) while (4) is not. - Let M be a simple right A-module. If x is a nonzero element in M, then the annihilator of x is a regular maximal right ideal in A.

