
Regular measure
Encyclopedia
In mathematics
, a regular measure on a topological space
is a measure
for which every measurable set is "approximately open" and "approximately closed".
and closed set
s are measurable sets, and Σ is at least as fine as the Borel σ-algebra on X). Let μ be a measure on (X, Σ). A measurable subset A of X is said to be μ-regular if
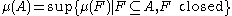
and
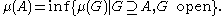
Alternatively, A is a μ-regular set if and only if
, for every δ > 0, there exists a closed set F and an open set G such that

and
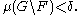
The two definitions are equivalent if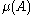 is finite (otherwise, the second definition is stronger). If every measurable set is regular, then the measure μ is said to be a regular measure.
is finite (otherwise, the second definition is stronger). If every measurable set is regular, then the measure μ is said to be a regular measure.
Some authors require the set F to be compact (not just closed).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a regular measure on a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
for which every measurable set is "approximately open" and "approximately closed".
Definition
Let (X, T) be a topological space and let Σ be a σ-algebra on X that contains the topology T (so that all openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
and closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s are measurable sets, and Σ is at least as fine as the Borel σ-algebra on X). Let μ be a measure on (X, Σ). A measurable subset A of X is said to be μ-regular if
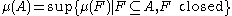
and
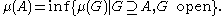
Alternatively, A is a μ-regular set if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
, for every δ > 0, there exists a closed set F and an open set G such that

and
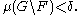
The two definitions are equivalent if
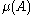 is finite (otherwise, the second definition is stronger). If every measurable set is regular, then the measure μ is said to be a regular measure.
is finite (otherwise, the second definition is stronger). If every measurable set is regular, then the measure μ is said to be a regular measure.Some authors require the set F to be compact (not just closed).
Examples
- Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on the real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
is a regular measure: see the regularity theorem for Lebesgue measureRegularity theorem for Lebesgue measureIn mathematics, the regularity theorem for Lebesgue measure is a result in measure theory that states that Lebesgue measure on the real line is a regular measure...
. - Any Borel probability measureProbability measureIn mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
on any metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
is a regular measure. - The trivial measureTrivial measureIn mathematics, specifically in measure theory, the trivial measure on any measurable space is the measure μ which assigns zero measure to every measurable set: μ = 0 for all A in Σ.-Properties of the trivial measure:...
, which assigns measure zero to every measurable subset, is a regular measure. - A trivial example of a non-regular measure on the real line with its usual topology is the measure μ where
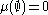 ,
,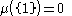 , and
, and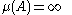 for any other set
for any other set 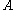 .
.

