
Regulated rewriting
Encyclopedia
Regulated rewriting is a specific area of formal languages studying grammatical systems which are able to take some kind of control over the production applied in a derivation step. For this reason, the grammatical systems studied in Regulated Rewriting theory are also called "Grammars with Controlled Derivations". Among such grammars can be noticed:
A Matrix Grammar,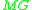 , is a four-tuple
, is a four-tuple 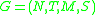 where
where
1.- is an alphabet of non-terminal symbols
is an alphabet of non-terminal symbols
2.-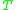 is an alphabet of terminal symbols disjoint with
is an alphabet of terminal symbols disjoint with 
3.-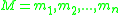 is a finite set of matrices, which are non-empty sequences
is a finite set of matrices, which are non-empty sequences
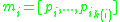 ,
,
with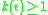 , and
, and
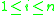 , where each
, where each
 , is an ordered pair
, is an ordered pair
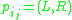
being
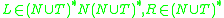
these pairs are called "productions", and are denoted
 . In these conditions the matrices can be written down as
. In these conditions the matrices can be written down as
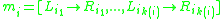
4.- S is the start symbol
Definition
Let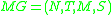 be a matrix grammar and let
be a matrix grammar and let 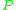
the collection of all productions on matrices of .
.
We said that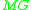 is of type i according to Chomsky's hierarchy with
is of type i according to Chomsky's hierarchy with 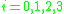 , or "increasing length"
, or "increasing length"
or "linear" or "without -productions" if and only if the grammar
-productions" if and only if the grammar 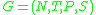 has the corresponding property.
has the corresponding property.
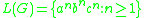
is generated by the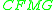
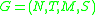 where
where
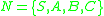 is the non-terminal set,
is the non-terminal set,
 is the terminal set,
is the terminal set,
and the set of matrices is defined as
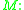
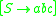 ,
,
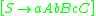 ,
,
 ,
,
 .
.
Definition
A Time Variant Grammar is a pair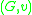 where
where 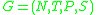
is a grammar and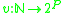 is a function from the set of natural
is a function from the set of natural
numbers to the class of subsets of the set the productions.
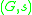 where
where 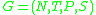
is a grammar and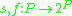 are the success and fail functions from the set of productions
are the success and fail functions from the set of productions
to the class of subsets of the set the productions.
A Grammar With Regular Control Language,
 , is a pair
, is a pair 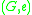 where
where 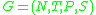
is a grammar and is a regular expression over the alphabet of the set the productions.
is a regular expression over the alphabet of the set the productions.
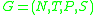 where
where
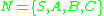 is the non-terminal set,
is the non-terminal set,
 is the terminal set,
is the terminal set,
and the productions set is defined as
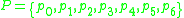
being

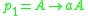 ,
,
 ,
,
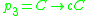
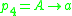 ,
,
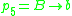 , and
, and
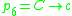 .
.
Clearly,
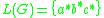 .
.
Now, considering the productions set
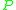 as an alphabet (since it is a finite set),
as an alphabet (since it is a finite set),
define the regular expression over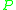 :
:
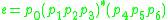 .
.
Combining the CFG grammar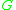 and the regular expression
and the regular expression
 , we obtain the CFGWRCL
, we obtain the CFGWRCL
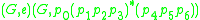
which generates the language
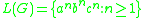 .
.
Besides there are other grammars with regulated rewriting, the four cited above are good examples of how to extend context-free grammars with some kind of control mechanism to obtain a Turing machine
powerful grammatical device.
Salomaa, Arto
Formal languages
Academic Press, 1973
ACM monograph series
[2]
G. Rozenberg, A. Salomaa, (eds.)
Handbook of formal languages
Berlin; New York : Springer, 1997
ISBN 3540614869 (set) (3540604200 : v. 1; 3540606483 : v. 2; 3540606491: v. 3)
[3]
Regulated Rewriting in Formal Language Theory
Jurgen Dassow; G. Paun
Pages: 308. Medium: Hardcover. Year of Publication: 1990
ISBN:0387514147. Springer-Verlag New York, Inc. Secaucus, NJ, USA
[4]
Grammars with Regulated Rewriting
Jurgen Dassow Otto-von-Guericke
Available at:
http://citeseer.ist.psu.edu/700926.html
and
http://theo.cs.uni-magdeburg.de/dassow_eng.html
(http://theo.cs.uni-magdeburg.de/dassow/tarraphd.pdf)
[5]
Some questions of language theory
S. Abraham
in Proceedings of the 1965 International Conference On Computational Linguistics
pp 1 - 11, Bonn, Germany Year of Publication: 1965
Available at:
http://acl.ldc.upenn.edu/C/C65/C65-1001.pdf
Basic concepts
DefinitionA Matrix Grammar,
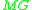 , is a four-tuple
, is a four-tuple 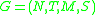 where
where1.-
 is an alphabet of non-terminal symbols
is an alphabet of non-terminal symbols2.-
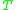 is an alphabet of terminal symbols disjoint with
is an alphabet of terminal symbols disjoint with 
3.-
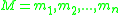 is a finite set of matrices, which are non-empty sequences
is a finite set of matrices, which are non-empty sequences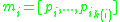 ,
,with
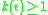 , and
, and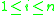 , where each
, where each , is an ordered pair
, is an ordered pair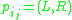
being
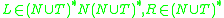
these pairs are called "productions", and are denoted
 . In these conditions the matrices can be written down as
. In these conditions the matrices can be written down as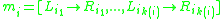
4.- S is the start symbol
Definition
Let
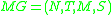 be a matrix grammar and let
be a matrix grammar and let 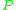
the collection of all productions on matrices of
 .
.We said that
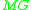 is of type i according to Chomsky's hierarchy with
is of type i according to Chomsky's hierarchy with 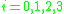 , or "increasing length"
, or "increasing length"or "linear" or "without
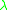 -productions" if and only if the grammar
-productions" if and only if the grammar 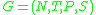 has the corresponding property.
has the corresponding property.The classic example (taken from [5] with change of nonterminals names)
The context-sensitive language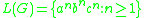
is generated by the
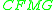
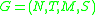 where
where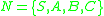 is the non-terminal set,
is the non-terminal set, is the terminal set,
is the terminal set,and the set of matrices is defined as
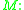
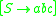 ,
,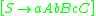 ,
, ,
, .
.Time Variant Grammars
Basic conceptsDefinition
A Time Variant Grammar is a pair
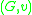 where
where 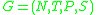
is a grammar and
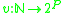 is a function from the set of natural
is a function from the set of naturalnumbers to the class of subsets of the set the productions.
Definition
A Programmed Grammar is a pair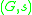 where
where 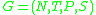
is a grammar and
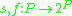 are the success and fail functions from the set of productions
are the success and fail functions from the set of productionsto the class of subsets of the set the productions.
Basic concepts
DefinitionA Grammar With Regular Control Language,
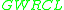 , is a pair
, is a pair 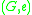 where
where 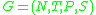
is a grammar and
 is a regular expression over the alphabet of the set the productions.
is a regular expression over the alphabet of the set the productions.A naive example
Consider the CFG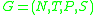 where
where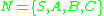 is the non-terminal set,
is the non-terminal set, is the terminal set,
is the terminal set,and the productions set is defined as
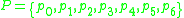
being

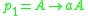 ,
, ,
,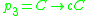
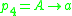 ,
,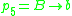 , and
, and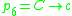 .
.Clearly,
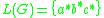 .
.Now, considering the productions set
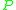 as an alphabet (since it is a finite set),
as an alphabet (since it is a finite set),define the regular expression over
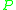 :
: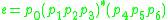 .
.Combining the CFG grammar
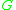 and the regular expression
and the regular expression , we obtain the CFGWRCL
, we obtain the CFGWRCL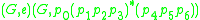
which generates the language
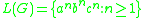 .
.Besides there are other grammars with regulated rewriting, the four cited above are good examples of how to extend context-free grammars with some kind of control mechanism to obtain a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
powerful grammatical device.
Sources
[1]Salomaa, Arto
Formal languages
Academic Press, 1973
ACM monograph series
[2]
G. Rozenberg, A. Salomaa, (eds.)
Handbook of formal languages
Berlin; New York : Springer, 1997
ISBN 3540614869 (set) (3540604200 : v. 1; 3540606483 : v. 2; 3540606491: v. 3)
[3]
Regulated Rewriting in Formal Language Theory
Jurgen Dassow; G. Paun
Pages: 308. Medium: Hardcover. Year of Publication: 1990
ISBN:0387514147. Springer-Verlag New York, Inc. Secaucus, NJ, USA
[4]
Grammars with Regulated Rewriting
Jurgen Dassow Otto-von-Guericke
Available at:
http://citeseer.ist.psu.edu/700926.html
and
http://theo.cs.uni-magdeburg.de/dassow_eng.html
(http://theo.cs.uni-magdeburg.de/dassow/tarraphd.pdf)
[5]
Some questions of language theory
S. Abraham
in Proceedings of the 1965 International Conference On Computational Linguistics
pp 1 - 11, Bonn, Germany Year of Publication: 1965
Available at:
http://acl.ldc.upenn.edu/C/C65/C65-1001.pdf

