
Reissner-Nordström metric
Encyclopedia
In physics
and astronomy
, the Reissner–Nordström metric is a static solution
to the Einstein-Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, spherically symmetric body of mass M.
and Gunnar Nordström
, their metric can be written as
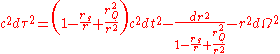
where
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, the Reissner–Nordström metric is a static solution
Static spacetime
In general relativity, a spacetime is said to be static if it admits a global, non-vanishing, timelike Killing vector field K which is irrotational, i.e., whose orthogonal distribution is involutive...
to the Einstein-Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, spherically symmetric body of mass M.
The metric
Discovered by Hans ReissnerHans Reissner
Hans Jacob Reissner was a German aeronautical engineer whose avocation was mathematical physics. During World War I he was awarded the Iron Cross second class for his pioneering work on aircraft design....
and Gunnar Nordström
Gunnar Nordström
Gunnar Nordström was a Finnish theoretical physicist best remembered for his theory of gravitation, which was an early competitor of general relativity...
, their metric can be written as
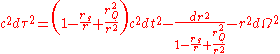
where
- τ is the proper time (time measured by a clock moving with the particle) in seconds,
- c is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in meters per second, - t is the time coordinate (measured by a stationary clock at infinity) in seconds,
- r is the radial coordinate (circumference of a circle centered on the star divided by 2π) in meters,
- Ω is the solid angleSolid angleThe solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point...
,
-
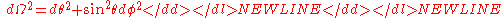
- rs is the Schwarzschild radiusSchwarzschild radiusThe Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
(in meters) of the massive body, which is related to its mass M by
-

- where G is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, and - rQ is a length-scale corresponding to the electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
Q of the mass
-
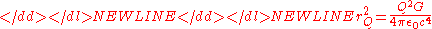
- where 1/4πε0 is Coulomb's force constantCoulomb's lawCoulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
.
The colors have been added in order to highlight the extensions to Minkowski spacetime. In the limit that the charge Q (or equivalently, the length-scale rQ) goes to zero, one recovers the Schwarzschild metricSchwarzschild metricIn Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
. To do this, you just remove term in . The classical Newtonian theory of gravity may then be recovered in the limit as the ratio rs/r goes to zero. To do this, you just remove term in
. The classical Newtonian theory of gravity may then be recovered in the limit as the ratio rs/r goes to zero. To do this, you just remove term in 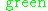 . In that limit, the metric returns to the Minkowski metric for special relativitySpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
. In that limit, the metric returns to the Minkowski metric for special relativitySpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...

In practice, the ratio rs/r is almost always extremely small. For example, the Schwarzschild radius rs of the EarthEarthEarth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
is roughly 9 mm (³⁄8 inchInchAn inch is the name of a unit of length in a number of different systems, including Imperial units, and United States customary units. There are 36 inches in a yard and 12 inches in a foot...
), whereas a satelliteSatelliteIn the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....
in a geosynchronous orbitGeosynchronous orbitA geosynchronous orbit is an orbit around the Earth with an orbital period that matches the Earth's sidereal rotation period...
has a radius r that is roughly four billion times larger, at 42,164 km (26,200 mileMileA mile is a unit of length, most commonly 5,280 feet . The mile of 5,280 feet is sometimes called the statute mile or land mile to distinguish it from the nautical mile...
s). Even at the surface of the Earth, the corrections to Newtonian gravity are only one part in a billion. The ratio only becomes large close to black holeBlack holeA black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s and other ultra-dense objects such as neutron starNeutron starA neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
s.
Charged black holes
Although charged black holes with are similar to the Schwarzschild black hole, they have two horizons: the event horizonEvent horizonIn general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
are similar to the Schwarzschild black hole, they have two horizons: the event horizonEvent horizonIn general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
and an internal Cauchy horizonCauchy horizonIn physics, a Cauchy horizon is a light-like boundary of the domain of validity of a Cauchy problem...
. As usual, the event horizons for the spacetime are located where diverges:
diverges:
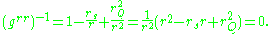
The second factor is a quadraticQuadratic equationIn mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
in r and we find its zeros by using the quadratic formula:

These concentric event horizonEvent horizonIn general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
s become degenerateDegenerate energy levelIn physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
for which corresponds to an extremal black holeExtremal black holeIn theoretical physics, an extremal black hole is a black hole with the minimal possible mass that can be compatible with a given charge and angular momentum . In other words, this is the smallest possible black hole that can exist while rotating at a given fixed constant speed.The concept of an...
which corresponds to an extremal black holeExtremal black holeIn theoretical physics, an extremal black hole is a black hole with the minimal possible mass that can be compatible with a given charge and angular momentum . In other words, this is the smallest possible black hole that can exist while rotating at a given fixed constant speed.The concept of an...
. Black holes with are believed not to exist in nature because they would contain a naked singularityNaked singularityIn general relativity, a naked singularity is a gravitational singularity, without an event horizon. In a black hole, there is a region around the singularity, the event horizon, where the gravitational force of the singularity is strong enough so that light cannot escape. Hence, the singularity...
are believed not to exist in nature because they would contain a naked singularityNaked singularityIn general relativity, a naked singularity is a gravitational singularity, without an event horizon. In a black hole, there is a region around the singularity, the event horizon, where the gravitational force of the singularity is strong enough so that light cannot escape. Hence, the singularity...
; their appearance would contradict Roger PenroseRoger PenroseSir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
's cosmic censorship hypothesisCosmic censorship hypothesisThe weak and the strong cosmic censorship hypotheses are two mathematical conjectures about the structure of singularities arising in general relativity....
which is generally believed to be true. Theories with supersymmetrySupersymmetryIn particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
usually guarantee that such "superextremal" black holes can't exist.
The electromagnetic potential is
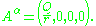
If magnetic monopoles are included into the theory, then a generalization to include magnetic charge is obtained by replacing
is obtained by replacing 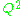 by
by 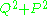 in the metric and including the term
in the metric and including the term 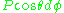 in the electromagnetic potential.
in the electromagnetic potential.
External links
- spacetime diagrams including Finkelstein diagram and Penrose diagramPenrose diagramIn theoretical physics, a Penrose diagram is a two-dimensional diagram that captures the causal relations between different points in spacetime...
, by Andrew J. S. Hamilton - "Particle Moving Around Two Extreme Black Holes" by Enrique Zeleny, The Wolfram Demonstrations Project.
- where 1/4πε0 is Coulomb's force constant
- where G is the gravitational constant
- rs is the Schwarzschild radius

