Residual property (mathematics)
Encyclopedia
In the mathematical
field of group theory
, a group is residually X (where X is some property of groups) if it "can be recovered from groups with property X".
Formally, a group G is residually X if for every non-trivial element g there is a homomorphism h from G to a group with property X such that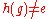
.
More categorically, a group is residually X if it embeds into its pro-X completion (see profinite group, pro-p group
), that is, the inverse limit
of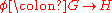
where H is a group with property X.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a group is residually X (where X is some property of groups) if it "can be recovered from groups with property X".
Formally, a group G is residually X if for every non-trivial element g there is a homomorphism h from G to a group with property X such that
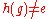.More categorically, a group is residually X if it embeds into its pro-X completion (see profinite group, pro-p group
Pro-p group
In mathematics, a pro-p group is a profinite group G such that for any open normal subgroup N\triangleleft G the quotient group G/N is a p-group...
), that is, the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of
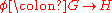where H is a group with property X.Examples
Important examples include:- Residually finiteResidually finite groupIn the mathematical field of group theory, a group G is residually finite or finitely approximable if for every nontrivial element g in G there is a homomorphism h from G to a finite group, such thath \neq 1.\,...
- Residually nilpotentNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
- Residually free groups