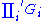Restricted product
Encyclopedia
The restricted product is a construction in the theory of topological group
s.
Let be an indexing set;
be an indexing set; 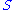 a finite subset of
a finite subset of 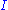 . If for each
. If for each  ,
, 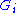 is a locally compact group, and for each
is a locally compact group, and for each 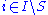 ,
,  is an open compact
is an open compact
subgroup, then the restricted product
is the subset of the product of the 's consisting of all elements
's consisting of all elements 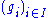 such that
such that 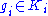 for all but finitely many
for all but finitely many 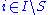 .
.
This group is given the topology whose basis of open sets are those of the form
where is open in
is open in 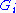 and
and 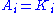 for all but finitely many
for all but finitely many 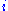 .
.
One can easily prove that the restricted product is itself a locally compact group. The best known example of this construction is that of the adele ring
and idele group of a global field
.
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s.
Let
 be an indexing set;
be an indexing set; 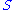 a finite subset of
a finite subset of 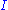 . If for each
. If for each  ,
, 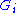 is a locally compact group, and for each
is a locally compact group, and for each 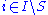 ,
,  is an open compact
is an open compactCompact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
subgroup, then the restricted product
is the subset of the product of the
 's consisting of all elements
's consisting of all elements 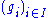 such that
such that 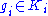 for all but finitely many
for all but finitely many 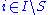 .
.This group is given the topology whose basis of open sets are those of the form
where
 is open in
is open in 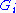 and
and 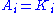 for all but finitely many
for all but finitely many 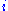 .
.One can easily prove that the restricted product is itself a locally compact group. The best known example of this construction is that of the adele ring
Adele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
and idele group of a global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
.