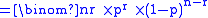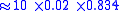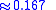Return period
Encyclopedia
A return period also known as a recurrence interval is an estimate of the interval of time between events like an earthquake
, flood
or river discharge flow
of a certain intensity or size. It is a statistical measurement denoting the average recurrence interval over an extended period of time, and is usually required for risk analysis (i.e. whether a project should be allowed to go forward in a zone of a certain risk) and also to dimension structures so that they are capable of withstanding an event of a certain return period (with its associated intensity).
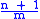
For floods, this is conventionally measured in terms of m³/s;
for storm surge
s, in terms of the height of the surge, and similarly for other events.
or 10% chance of being exceeded in any one year and a 50-year flood has a 0.02 or 2% chance of being exceeded in any one year.
While it is true that a 10-year event will occur, on average, once every 10 years and that a 100-year event is so large that we expect it only to occur every 100 years, this is only a statistical statement: the expected number of 100-year events in an n year period is n/100, in the sense of expected value
.
Similarly, the expected time until another 100-year event is 100 years, and if in a given year or years the event does not occur, the expected time until it occurs remains 100 years, with this "100 years" resetting each time.
It does not mean that 100-year floods will happen regularly, every 100 years,
despite the connotations of the name "return period": in any given 100-year period, a 100-year storm may occur once, twice, more, or not at all, and each outcome has a probability that can be computed as below.
Note also that the estimated return period below is a statistic
: it is computed from a set of data (the observations), as distinct from the theoretical value in an idealized distribution. One does not actually know that a certain magnitude or greater happens with 1% probability, only that it has been observed exactly once in 100 years.
This distinction is significant because there are few observations of rare events: for instance if observations go back 400 years, the most extreme event (a 400-year event by the statistical definition) may later be classed, on longer observation, as a 200-year event (if a comparable event immediately occurs) or a 500-year event (if no comparable event occurs for 100 years).
Further, one cannot determine the size of a 1,000-year event based on such records alone, but instead must use a statistical model
to predict the magnitude of such an (unobserved) event.
.
Take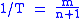
where
If the probability of an event occurring is p, then the probability of the event not occurring is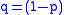
.
The binomial distribution can be used to find the probability of occurrence of an event r times in a period of n years.
.
So the probability that such an event occurs exactly once in 10 successive years is;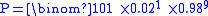
This is the likelihood of at least one event that exceeds design limits during the expected life of the structure: it is the complement of the likelihood that no events exceed design limits.
The equation for assessing this risk can be expressed as
where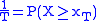
is the expression for the probability of the occurrence for the hydrologic event in question;
Earthquake
An earthquake is the result of a sudden release of energy in the Earth's crust that creates seismic waves. The seismicity, seismism or seismic activity of an area refers to the frequency, type and size of earthquakes experienced over a period of time...
, flood
Flood
A flood is an overflow of an expanse of water that submerges land. The EU Floods directive defines a flood as a temporary covering by water of land not normally covered by water...
or river discharge flow
Discharge (hydrology)
In hydrology, discharge is the volume rate of water flow, including any suspended solids , dissolved chemical species and/or biologic material , which is transported through a given cross-sectional area...
of a certain intensity or size. It is a statistical measurement denoting the average recurrence interval over an extended period of time, and is usually required for risk analysis (i.e. whether a project should be allowed to go forward in a zone of a certain risk) and also to dimension structures so that they are capable of withstanding an event of a certain return period (with its associated intensity).
Equation
Recurrence interval =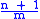- n is number of years on record;
- m is the rank of the event being considered
For floods, this is conventionally measured in terms of m³/s;
for storm surge
Storm surge
A storm surge is an offshore rise of water associated with a low pressure weather system, typically tropical cyclones and strong extratropical cyclones. Storm surges are caused primarily by high winds pushing on the ocean's surface. The wind causes the water to pile up higher than the ordinary sea...
s, in terms of the height of the surge, and similarly for other events.
Return period as "expected frequency"
The theoretical return period is the inverse of the probability that the event will be exceeded in any one year. For example, a 10-year flood has a or 10% chance of being exceeded in any one year and a 50-year flood has a 0.02 or 2% chance of being exceeded in any one year.While it is true that a 10-year event will occur, on average, once every 10 years and that a 100-year event is so large that we expect it only to occur every 100 years, this is only a statistical statement: the expected number of 100-year events in an n year period is n/100, in the sense of expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
.
Similarly, the expected time until another 100-year event is 100 years, and if in a given year or years the event does not occur, the expected time until it occurs remains 100 years, with this "100 years" resetting each time.
It does not mean that 100-year floods will happen regularly, every 100 years,
despite the connotations of the name "return period": in any given 100-year period, a 100-year storm may occur once, twice, more, or not at all, and each outcome has a probability that can be computed as below.
Note also that the estimated return period below is a statistic
Statistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
: it is computed from a set of data (the observations), as distinct from the theoretical value in an idealized distribution. One does not actually know that a certain magnitude or greater happens with 1% probability, only that it has been observed exactly once in 100 years.
This distinction is significant because there are few observations of rare events: for instance if observations go back 400 years, the most extreme event (a 400-year event by the statistical definition) may later be classed, on longer observation, as a 200-year event (if a comparable event immediately occurs) or a 500-year event (if no comparable event occurs for 100 years).
Further, one cannot determine the size of a 1,000-year event based on such records alone, but instead must use a statistical model
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
to predict the magnitude of such an (unobserved) event.
Probability distribution
In a given period of n years, the probability of a given number k of events of a given return interval T is given by the binomial distribution as follows. In the limit of long periods (as n grows large), this converges to the Poisson distributionPoisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
.
Take
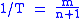
where
- T is return interval
- m is ranking
- n is number of occurrences
If the probability of an event occurring is p, then the probability of the event not occurring is
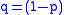.The binomial distribution can be used to find the probability of occurrence of an event r times in a period of n years.
Example
Given that the return period of an event is 50 years,.So the probability that such an event occurs exactly once in 10 successive years is;
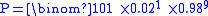
Risk analysis
Return period is also useful for risk analysis (such as natural, inherent, or hydrologic risk of failure). When dealing with a structure design expectations the return period is useful in calculating the risk of the structure with respect to a given storm return period when given the design life expectation.This is the likelihood of at least one event that exceeds design limits during the expected life of the structure: it is the complement of the likelihood that no events exceed design limits.
The equation for assessing this risk can be expressed as
where
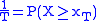is the expression for the probability of the occurrence for the hydrologic event in question;
- n is the expected life of the structure.
External links
- CumFreq, a computer program for cumulative frequencies, return periods, and confidence intervals