
Riemann invariant
Encyclopedia
Riemann invariants are mathematical transformations made on a a system of quasi-linear
first order partial differential equation
s to make them more easily solvable. Riemann invariants are constant along the characteristic curves
of the partial differential equations where they obtain the name invariant
. They were first obtained by Bernhard Riemann
in his work on plane waves in gas dynamics.
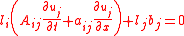
where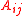 and
and  are the elements of the matrices
are the elements of the matrices
 and
and  where
where 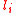 and
and 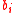 are elements of vector
are elements of vector
s. It will be asked if it is possible to rewrite this equation to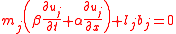
To do this curves will be introduced in the plane defined by the vector field
plane defined by the vector field
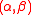 . The term in the brackets will be rewritten in terms of a total derivative
. The term in the brackets will be rewritten in terms of a total derivative
where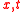 are parametrized as
are parametrized as 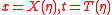
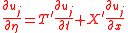
comparing the last two equations we find
which can be now written in characteristic form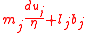
where we must have the conditions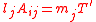 ,
, 
where can be eliminated to give the necessary condition
can be eliminated to give the necessary condition
so for a nontrival solution is the determinant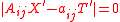
For Riemann invariants we are concerned with the case when the matrix is an identity matrix
is an identity matrix
to form
notice this is homogeneous due to the vector being zero. In characteristic form the system is
being zero. In characteristic form the system is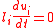 with
with 
Where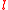 is the left eigenvector of the matrix
is the left eigenvector of the matrix  and
and 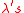 is the characteristic speeds of the eigenvalues of the matrix
is the characteristic speeds of the eigenvalues of the matrix  which satisfy
which satisfy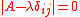
To simplify these characteristic equations we can make the transformations such that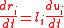
which form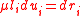
An integrating factor
 can be multiplied in to help integrate this. So the system now has the characteristic form
can be multiplied in to help integrate this. So the system now has the characteristic form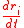 on
on 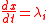
which is equivalent to the diagonal system
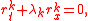
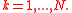
The solution of this system can be given by the generalized hodograph method.

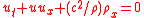
write this system in matrix form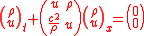
where the matrix from the analysis above the eigenvalues and eigenvectors need to be found.The eigenvalues are found to satisfy
from the analysis above the eigenvalues and eigenvectors need to be found.The eigenvalues are found to satisfy
to give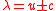
and the eigenvectors are found to be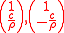
where the riemann invariants are
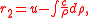
In shallow water equations there is the relation to give the riemann invariants
to give the riemann invariants

to give the equations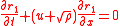

Which can be solved by the hodograph transformation. If the matrix form of the system of pde's is in the form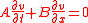
Then it may be possible to multiply across by the inverse matrix so long as the matrix determinant
so long as the matrix determinant
of is not zero.
is not zero.
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
first order partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s to make them more easily solvable. Riemann invariants are constant along the characteristic curves
Method of characteristics
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
of the partial differential equations where they obtain the name invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
. They were first obtained by Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
in his work on plane waves in gas dynamics.
Mathematical theory
Consider the set of hyperbolic partial differential equations of the form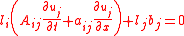
where
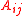 and
and  are the elements of the matrices
are the elements of the matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
 and
and  where
where 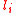 and
and 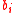 are elements of vector
are elements of vectorVector
Vector, a Latin word meaning "carrier", may refer in English to:-In computer science:*A one-dimensional array**Vector , a data type in the C++ Standard Template Library...
s. It will be asked if it is possible to rewrite this equation to
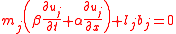
To do this curves will be introduced in the
 plane defined by the vector field
plane defined by the vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
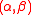 . The term in the brackets will be rewritten in terms of a total derivative
. The term in the brackets will be rewritten in terms of a total derivativeTotal derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
where
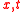 are parametrized as
are parametrized as 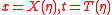
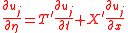
comparing the last two equations we find

which can be now written in characteristic form
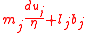
where we must have the conditions
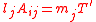 ,
, 
where
 can be eliminated to give the necessary condition
can be eliminated to give the necessary condition
so for a nontrival solution is the determinant
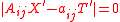
For Riemann invariants we are concerned with the case when the matrix
 is an identity matrix
is an identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
to form

notice this is homogeneous due to the vector
 being zero. In characteristic form the system is
being zero. In characteristic form the system is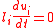 with
with 
Where
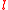 is the left eigenvector of the matrix
is the left eigenvector of the matrix  and
and 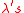 is the characteristic speeds of the eigenvalues of the matrix
is the characteristic speeds of the eigenvalues of the matrix  which satisfy
which satisfy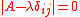
To simplify these characteristic equations we can make the transformations such that
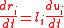
which form
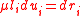
An integrating factor
Integrating factor
In mathematics, an integrating factor is a function that is chosen to facilitate the solving of a given equation involving differentials. It is commonly used to solve ordinary differential equations, but is also used within multivariable calculus, in this case often multiplying through by an...
 can be multiplied in to help integrate this. So the system now has the characteristic form
can be multiplied in to help integrate this. So the system now has the characteristic form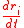 on
on 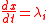
which is equivalent to the diagonal system
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
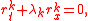
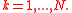
The solution of this system can be given by the generalized hodograph method.
Example
Consider the shallow water equationsShallow water equations
The shallow water equations are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid .The equations are derived from depth-integrating the Navier–Stokes...

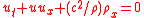
write this system in matrix form
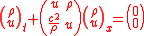
where the matrix
 from the analysis above the eigenvalues and eigenvectors need to be found.The eigenvalues are found to satisfy
from the analysis above the eigenvalues and eigenvectors need to be found.The eigenvalues are found to satisfy
to give
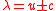
and the eigenvectors are found to be
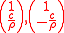
where the riemann invariants are

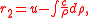
In shallow water equations there is the relation
 to give the riemann invariants
to give the riemann invariants

to give the equations
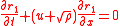

Which can be solved by the hodograph transformation. If the matrix form of the system of pde's is in the form
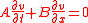
Then it may be possible to multiply across by the inverse matrix
 so long as the matrix determinant
so long as the matrix determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of
 is not zero.
is not zero.

