
Riesz mean
Encyclopedia
In mathematics
, the Riesz mean is a certain mean
of the terms in a series
. They were introduced by Marcel Riesz
in 1911 as an improvement over the Cesàro mean. The Riesz mean should not be confused with the Bochner–Riesz mean or the Strong–Riesz mean.
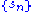 , the Riesz mean of the series is defined by
, the Riesz mean of the series is defined by
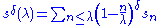
Sometimes, a generalized Riesz mean is defined as
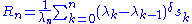
Here, the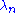 are sequence with
are sequence with  and with
and with 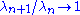 as
as 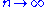 . Other than this, the
. Other than this, the 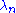 are otherwise taken as arbitrary.
are otherwise taken as arbitrary.
Riesz means are often used to explore the summability of sequences; typical summability theorems discuss the case of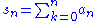 for some sequence
for some sequence 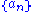 . Typically, a sequence is summable when the limit
. Typically, a sequence is summable when the limit 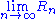 exists, or the limit
exists, or the limit 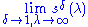 exists, although the precise summability theorems in question often impose additional conditions.
exists, although the precise summability theorems in question often impose additional conditions.
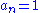 for all
for all  . Then
. Then
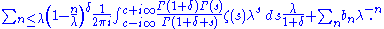
Here, one must take ;
; 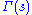 is the Gamma function
is the Gamma function
and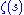 is the Riemann zeta function. The power series
is the Riemann zeta function. The power series
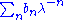
can be shown to be convergent for . Note that the integral is of the form of an inverse Mellin transform
. Note that the integral is of the form of an inverse Mellin transform
.
Another interesting case connected with number theory
arises by taking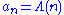 where
where 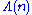 is the Von Mangoldt function
is the Von Mangoldt function
. Then
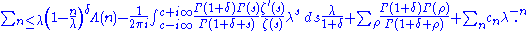
Again, one must take c > 1. The sum over ρ is the sum over the zeroes of the Riemann zeta function, and
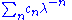
is convergent for λ > 1.
The integrals that occur here are similar to the Nörlund–Rice integral; very roughly, they can be connected to that integral via Perron's formula
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Riesz mean is a certain mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of the terms in a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
. They were introduced by Marcel Riesz
Marcel Riesz
Marcel Riesz was a Hungarian mathematician who was born in Győr, Hungary . He moved to Sweden in 1908 and spent the rest of his life there, dying in Lund, where he was a professor from 1926 at Lund University...
in 1911 as an improvement over the Cesàro mean. The Riesz mean should not be confused with the Bochner–Riesz mean or the Strong–Riesz mean.
Definition
Given a series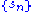 , the Riesz mean of the series is defined by
, the Riesz mean of the series is defined by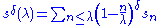
Sometimes, a generalized Riesz mean is defined as
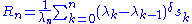
Here, the
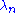 are sequence with
are sequence with  and with
and with 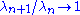 as
as 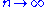 . Other than this, the
. Other than this, the 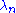 are otherwise taken as arbitrary.
are otherwise taken as arbitrary.Riesz means are often used to explore the summability of sequences; typical summability theorems discuss the case of
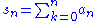 for some sequence
for some sequence 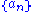 . Typically, a sequence is summable when the limit
. Typically, a sequence is summable when the limit 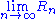 exists, or the limit
exists, or the limit 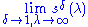 exists, although the precise summability theorems in question often impose additional conditions.
exists, although the precise summability theorems in question often impose additional conditions.Special cases
Let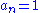 for all
for all  . Then
. Then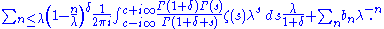
Here, one must take
 ;
; 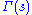 is the Gamma function
is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
and
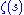 is the Riemann zeta function. The power series
is the Riemann zeta function. The power series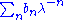
can be shown to be convergent for
 . Note that the integral is of the form of an inverse Mellin transform
. Note that the integral is of the form of an inverse Mellin transformMellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
.
Another interesting case connected with number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
arises by taking
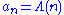 where
where 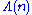 is the Von Mangoldt function
is the Von Mangoldt functionVon Mangoldt function
In mathematics, the von Mangoldt function is an arithmetic function named after German mathematician Hans von Mangoldt.-Definition:The von Mangoldt function, conventionally written as Λ, is defined as...
. Then
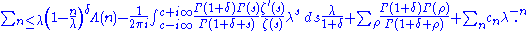
Again, one must take c > 1. The sum over ρ is the sum over the zeroes of the Riemann zeta function, and
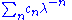
is convergent for λ > 1.
The integrals that occur here are similar to the Nörlund–Rice integral; very roughly, they can be connected to that integral via Perron's formula
Perron's formula
In mathematics, and more particularly in analytic number theory, Perron's formula is a formula due to Oskar Perron to calculate the sum of an arithmetical function, by means of an inverse Mellin transform.-Statement:...
.

