
Robotics conventions
Encyclopedia
There are many conventions used in the robotics research field. This article summarises these conventions.
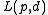 is completely defined by the ordered set of two vectors:
is completely defined by the ordered set of two vectors:
Each point on the line is given a parameter value
on the line is given a parameter value  that satisfies:
that satisfies:
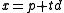 . The parameter t is unique once
. The parameter t is unique once 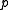 and
and 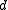 are chosen.
are chosen.
The representation is not minimal, because it uses six parameters for only four degrees of freedom.
is not minimal, because it uses six parameters for only four degrees of freedom.
The following two constraints apply:
The Plücker representation is denoted by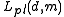 . Both
. Both  and
and 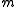 are free vectors:
are free vectors: 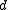 represents the direction of the line and
represents the direction of the line and 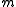 is the moment of
is the moment of 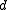 about the chosen reference origin.
about the chosen reference origin. (
(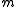 is independent of which point
is independent of which point 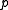 on the line is chosen!)
on the line is chosen!)
The advantage of the Plücker coordinates is that they are homogenous.
A line in Plücker coordinates has still four out of six independent parameters, so it is not a minimal representation. The two constraints on the six Plücker coordinates are
between two lines was the main geometric concept that allowed Denavit and Hartenberg to find a minimal representation. Engineers use the Denavit–Hartenberg convention(D–H) to help them describe the positions of links and joints unambiguously. Every link gets its own coordinate system
. There are a few rules to consider in choosing the coordinate system:
Once the coordinate frames are determined, inter-link transformations are uniquely described by the following four parameters:
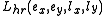 , is another minimal line representation, with parameters:
, is another minimal line representation, with parameters:
This representation is unique for a directed line. The coordinate singularities are different from the DH singularities: it has singularities if the line becomes parallel to either the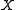 or
or 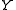 axis of the world frame.
axis of the world frame.
Line representations
Lines are very important in robotics because:- They model joint axes: a revolute jointRevolute jointA revolute joint is a one degree of freedom kinematic pair used in mechanisms. Revolute joints provide single-axis rotation function used in many places such as door hinges, folding mechanisms, and other uni-axial rotation devices. -See also:* Cylindrical joint* Kinematics* Degrees of freedom *...
makes any connected rigid body rotate about the line of its axis; a prismatic jointPrismatic jointA prismatic joint provides a linear sliding movement between two bodies, and is often called a slider, as in the slider-crank linkage. A prismatic joint is formed with a polygonal cross-section to resist rotation...
makes the connected rigid body translate along its axis line. - They model edges of the polyhedral objects used in many task planners or sensor processing modules.
- They are needed for shortest distance calculation between robots and obstacles
Non-minimal vector coordinates
A line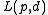 is completely defined by the ordered set of two vectors:
is completely defined by the ordered set of two vectors:
- a point vector
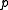 , indicating the position of an arbitrary point on
, indicating the position of an arbitrary point on 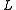
- one free direction vector
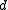 , giving the line a direction as well as a sense.
, giving the line a direction as well as a sense.
Each point
 on the line is given a parameter value
on the line is given a parameter value  that satisfies:
that satisfies: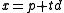 . The parameter t is unique once
. The parameter t is unique once 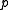 and
and 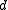 are chosen.
are chosen.The representation
 is not minimal, because it uses six parameters for only four degrees of freedom.
is not minimal, because it uses six parameters for only four degrees of freedom.The following two constraints apply:
- The direction vector
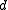 can be chosen to be a unit vector
can be chosen to be a unit vector - the point vector
 can be chosen to be the point on the line that is nearest the origin. So
can be chosen to be the point on the line that is nearest the origin. So 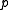 is orthogonal to
is orthogonal to 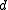
Plücker coordinates
Arthur Cayley and Julius Plücker introduced an alternative representation using two free vectors. This representation was finally named after Plücker.The Plücker representation is denoted by
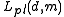 . Both
. Both  and
and 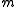 are free vectors:
are free vectors: 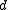 represents the direction of the line and
represents the direction of the line and 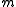 is the moment of
is the moment of 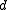 about the chosen reference origin.
about the chosen reference origin. (
(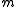 is independent of which point
is independent of which point 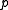 on the line is chosen!)
on the line is chosen!)The advantage of the Plücker coordinates is that they are homogenous.
A line in Plücker coordinates has still four out of six independent parameters, so it is not a minimal representation. The two constraints on the six Plücker coordinates are
- the homogeneity constraint
- the orthogonality constraint
Minimal line representation
A line representation is minimal if it uses four parameters, which is the minimum needed to represent all possible lines in the Euclidean Space (E³).Denavit–Hartenberg line coordinates
Jaques Denavit and Richard S. Hartenberg presented the first minimal representation for a line which is now widely used. The common normalCommon normal (robotics)
In robotics the common normal of two non-intersecting joint axes is a line perpendicular to both axes.The common normal can be used to characterize robot arm links, by using the "common normal distance" and the angle between the link axes in a plane perpendicular to the common normal...
between two lines was the main geometric concept that allowed Denavit and Hartenberg to find a minimal representation. Engineers use the Denavit–Hartenberg convention(D–H) to help them describe the positions of links and joints unambiguously. Every link gets its own coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
. There are a few rules to consider in choosing the coordinate system:
- the
 -axis is in the direction of the joint axis
-axis is in the direction of the joint axis - the
 -axis is parallel to the common normal:
-axis is parallel to the common normal: 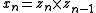
If there is no unique common normal (parallel axes), then
axes), then  (below) is a free parameter.
(below) is a free parameter. - the
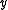 -axis follows from the
-axis follows from the  - and
- and  -axis by choosing it to be a right-handed coordinate system.
-axis by choosing it to be a right-handed coordinate system.
Once the coordinate frames are determined, inter-link transformations are uniquely described by the following four parameters:
-
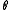 : angle about previous
: angle about previous  , from old
, from old  to new
to new 
-
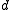 : offset along previous
: offset along previous  to the common normal
to the common normal -
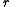 : length of the common normal (aka
: length of the common normal (aka  , but if using this notation, do not confuse with
, but if using this notation, do not confuse with  ). Assuming a revolute joint, this is the radius about previous
). Assuming a revolute joint, this is the radius about previous  .
. -
 : angle about common normal, from old
: angle about common normal, from old  axis to new
axis to new  axis
axis
Hayati–Roberts line coordinates
The Hayati–Roberts line representation, denoted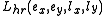 , is another minimal line representation, with parameters:
, is another minimal line representation, with parameters:
-
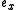 and
and 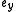 are the
are the 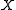 and
and 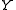 components of a unit direction vector
components of a unit direction vector  on the line. This requirement eliminates the need for a
on the line. This requirement eliminates the need for a 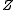 component, since
component, since 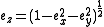
-
 and
and 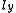 are the coordinates of the intersection point of the line with the plane through the origin of the world reference frame, and normal to the line. The reference frame on this normal plane has the same origin as the world reference frame, and its
are the coordinates of the intersection point of the line with the plane through the origin of the world reference frame, and normal to the line. The reference frame on this normal plane has the same origin as the world reference frame, and its 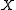 and
and 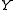 frame axes are images of the world frame's
frame axes are images of the world frame's  and
and 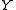 axes through parallel projection along the line.
axes through parallel projection along the line.
This representation is unique for a directed line. The coordinate singularities are different from the DH singularities: it has singularities if the line becomes parallel to either the
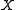 or
or 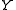 axis of the world frame.
axis of the world frame.
