
Rogers polynomials
Encyclopedia
In mathematics, the Rogers polynomials, also called Rogers–Askey–Ismail polynomials and continuous q-ultraspherical polynomials, are a family of orthogonal polynomials
introduced by in the course of his work on the Rogers–Ramanujan identities. They are q-analogs of ultraspherical polynomials, and are the Macdonald polynomials for the special case of the A1 affine root system
.
and discuss the properties of Rogers polynomials in detail.
by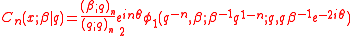
where x = cos(θ).
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
introduced by in the course of his work on the Rogers–Ramanujan identities. They are q-analogs of ultraspherical polynomials, and are the Macdonald polynomials for the special case of the A1 affine root system
Affine root system
In mathematics, an affine root system is a root system of affine-linear functions on a Euclidean space. They are used in the classification of affine Lie algebras and superalgebras, and semisimple p-adic algebraic groups, and correspond to families of Macdonald polynomials. The reduced affine root...
.
and discuss the properties of Rogers polynomials in detail.
Definition
The Rogers polynomials can be defined in terms of the descending Pochhammer symbol and the basic hypergeometric seriesBasic hypergeometric series
In mathematics, Heine's basic hypergeometric series, or hypergeometric q-series, are q-analog generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series....
by
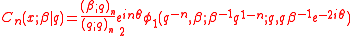
where x = cos(θ).

