
Root system of a semi-simple Lie algebra
Encyclopedia
In mathematics, there is a one-to-one correspondence between reduced crystallographic root system
s and semi-simple Lie algebras. We show the construction of a root system from a semi-simple Lie algebra and conversely, the construction of a semi-simple Lie algebra from a reduced crystallographic root system.
. Let further h be a Cartan subalgebra of g, i.e. a maximal abelian
subalgebra. Then h acts on g via simultaneously diagonalizable linear maps in the adjoint representation. For λ in h* define
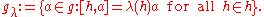
We call a non-zero λ in h* a root if gλ is nontrivial. gλ is called the root space of λ. Obviously g0 = h. One can show that each non-trivial gλ is one-dimensional. Let R be the set of all roots. Since the elements of h are simultaneously diagonalizable, we have
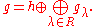
The Cartan subalgebra h inherits an inner product from the Killing form
on g. This induces an inner product on h*. One can show that with respect to this inner product R is a reduced crystallographic root lattice.

with the Chevalley-Serre relations
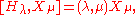



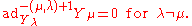
It turns out that the generated Lie algebra is semi-simple and has root system isomorphic to the given R.
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
s and semi-simple Lie algebras. We show the construction of a root system from a semi-simple Lie algebra and conversely, the construction of a semi-simple Lie algebra from a reduced crystallographic root system.
Associated root system
Let g be a semi-simple complex Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. Let further h be a Cartan subalgebra of g, i.e. a maximal abelian
Abelian
In mathematics, Abelian refers to any of number of different mathematical concepts named after Niels Henrik Abel:- Group theory :*Abelian group, a group in which the binary operation is commutative...
subalgebra. Then h acts on g via simultaneously diagonalizable linear maps in the adjoint representation. For λ in h* define
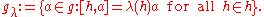
We call a non-zero λ in h* a root if gλ is nontrivial. gλ is called the root space of λ. Obviously g0 = h. One can show that each non-trivial gλ is one-dimensional. Let R be the set of all roots. Since the elements of h are simultaneously diagonalizable, we have
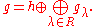
The Cartan subalgebra h inherits an inner product from the Killing form
Killing form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
on g. This induces an inner product on h*. One can show that with respect to this inner product R is a reduced crystallographic root lattice.
Associated semi-simple Lie algebra
Let E be a Euclidean space and R a reduced crystallographic root system in E. Let moreover Δ be a subset of positive roots. We define a complex Lie algebra over the generators
with the Chevalley-Serre relations

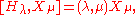



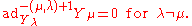
It turns out that the generated Lie algebra is semi-simple and has root system isomorphic to the given R.

