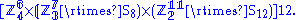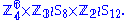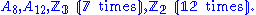Rubik's Cube group
Encyclopedia
The Rubik's Cube group is a mathematical group
which corresponds
to the set of all cube operations on Rubik's Cube
, with function composition
(chaining moves) as the group operation.
Any set of operations which returns the cube to the solved state, from the solved state, should be thought of as the identity transformation (the operation that does nothing). Any set of operations which solves the cube from a scrambled state should be thought of as an inverse transformation of the given scrambled state, since it returns the identity transformation.
s: identity
, inverse
, closure
, associativity
. It has an identity, simply not manipulating the cube. It has an inverse: by reversing a move sequence, the cube will return to its original position. It has closure: simpler sequences of moves combine to form a more complex move. Finally, it has associativity because doing different moves together, but in the same order, does not change the pattern.
. A 3×3×3 Rubik's cube consists of 6 faces, each with 9 colored squares called facets for a total of 54 facets. As the 6 facets in the centre of the faces are not moved by any cube operation, there are a total of 48 facets which actually change position.
Rotations of the centre facets are unimportant on the standard cube, but are crucial when considering non-standard incarnations such as Rubik's calendar and Rubik's world.
of the full symmetric group
S48 generated by the 6 face rotations.
of the cube group G is then equal to the number of possible positions attainable by the cube. This is:
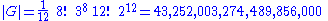
which factorizes
as
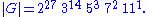
Because of the large size of the cube group, it is sometimes useful to analyse the structure with the assistance of a computer algebra system
.
In the following, we assume the notation described in How to solve the Rubik's Cube. Also we assume the orientation of the six centre facets to be fixed.
We consider two subgroups of G: First the group of cube orientations, Co, which leaves every block fixed, but can change its orientation. This group is a normal subgroup
of G. It can be represented as the normal closure of some operations that flip a few edges or twist a few corners. For example, it is the normal closure of the following two operations:
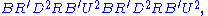(twist two corners)
(flip two edges).
For the second group we take G permutations, Cp, which can move the blocks around, but leaves the orientation fixed. For this subgroup there are more choices, depending on the precise way you fix the orientation. One choice is the following group, given by generators (the last generator is a 3 cycle on the edges):
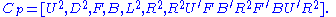
Since Co is a normal subgroup, the intersection of Co and Cp is the identity, and their product is the whole cube group, it follows that the cube group G is the semi-direct product of these two groups. That is
(For technical reasons, the above analysis is not correct. However, the possible permutations of the cubes, even when ignoring the orientations of the said cubes, is at the same time no bigger than Cp and at least as big as Cp, and this means that the cube group is the semi-direct product given above.)
Next we can take a closer look at these two groups. Co is
an abelian group
, it is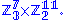
Cube permutations, Cp, is little more complicated. It has the following two normal subgroups, the group of even permutations on the corners A8 and the group of even permutations on the edges A12. Complementary to these two groups we can take a permutation that swaps two corners and swaps two edges. We obtain that
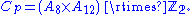
Putting all the pieces together we get that the cube group is isomorphic to
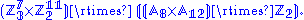
This group can also be described as the subdirect product
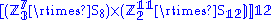, in the notation of Griess.
of
(This unimportance of centre facet rotations is an implicit example of a quotient group
at work, shielding the reader from the full automorphism group of the object in question.)
The symmetry group of the Rubik's cube obtained by dismembering it and reassembling is slightly larger: namely it is the direct product
The first factor is accounted for solely by rotations of the centre pieces, the second solely by symmetries of the corners, and the third solely by symmetries of the edges. The latter two factors are examples of wreath product
s.
The simple group
s that occur as quotients in the composition series
of the standard cube group (i.e. ignoring centre piece rotations) are
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
which corresponds
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the set of all cube operations on Rubik's Cube
Rubik's Cube
Rubik's Cube is a 3-D mechanical puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik.Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 and won the German Game of the Year special award for Best Puzzle that...
, with function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
(chaining moves) as the group operation.
Any set of operations which returns the cube to the solved state, from the solved state, should be thought of as the identity transformation (the operation that does nothing). Any set of operations which solves the cube from a scrambled state should be thought of as an inverse transformation of the given scrambled state, since it returns the identity transformation.
Group axioms
The Rubik's cube shares the axioms with mathematical groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s: identity
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
, inverse
Inverse (mathematics)
In many contexts in mathematics the term inverse indicates the opposite of something. This word and its derivatives are used widely in mathematics, as illustrated below....
, closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
, associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
. It has an identity, simply not manipulating the cube. It has an inverse: by reversing a move sequence, the cube will return to its original position. It has closure: simpler sequences of moves combine to form a more complex move. Finally, it has associativity because doing different moves together, but in the same order, does not change the pattern.
Objects
Formally, the Rubik's Cube group can be best understood as a permutation groupPermutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
. A 3×3×3 Rubik's cube consists of 6 faces, each with 9 colored squares called facets for a total of 54 facets. As the 6 facets in the centre of the faces are not moved by any cube operation, there are a total of 48 facets which actually change position.
Rotations of the centre facets are unimportant on the standard cube, but are crucial when considering non-standard incarnations such as Rubik's calendar and Rubik's world.
Operations
The cube operations consist of rotating the 6 faces and thereby permuting the 48 movable facets. By definition, each element of the cube group is a permutation of the 48 movable facets. However, there is a one-to-one correspondence between elements of the cube group and legal positions of the Rubik's cube. Any element of the cube group is a permutation that when applied to the solved cube results in a (legal) cube position. Conversely, any legal cube position must be the result of some sequence of face rotations applied to the solved cube, and any such sequence composition is an element of the cube group. The cube group G can then be defined as the subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the full symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
S48 generated by the 6 face rotations.
Total number
The orderOrder (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of the cube group G is then equal to the number of possible positions attainable by the cube. This is:
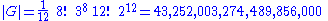
which factorizes
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
as
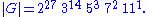
Because of the large size of the cube group, it is sometimes useful to analyse the structure with the assistance of a computer algebra system
Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
.
Structure
In the following, we assume the notation described in How to solve the Rubik's Cube. Also we assume the orientation of the six centre facets to be fixed.
We consider two subgroups of G: First the group of cube orientations, Co, which leaves every block fixed, but can change its orientation. This group is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of G. It can be represented as the normal closure of some operations that flip a few edges or twist a few corners. For example, it is the normal closure of the following two operations:
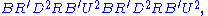(twist two corners) (flip two edges).For the second group we take G permutations, Cp, which can move the blocks around, but leaves the orientation fixed. For this subgroup there are more choices, depending on the precise way you fix the orientation. One choice is the following group, given by generators (the last generator is a 3 cycle on the edges):
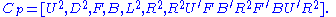
Since Co is a normal subgroup, the intersection of Co and Cp is the identity, and their product is the whole cube group, it follows that the cube group G is the semi-direct product of these two groups. That is
(For technical reasons, the above analysis is not correct. However, the possible permutations of the cubes, even when ignoring the orientations of the said cubes, is at the same time no bigger than Cp and at least as big as Cp, and this means that the cube group is the semi-direct product given above.)
Next we can take a closer look at these two groups. Co is
an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, it is
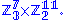
Cube permutations, Cp, is little more complicated. It has the following two normal subgroups, the group of even permutations on the corners A8 and the group of even permutations on the edges A12. Complementary to these two groups we can take a permutation that swaps two corners and swaps two edges. We obtain that
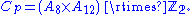
Putting all the pieces together we get that the cube group is isomorphic to
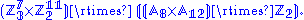
This group can also be described as the subdirect product
Subdirect product
In mathematics, especially in the areas of abstract algebra known as universal algebra, group theory, ring theory, and module theory, a subdirect product is a subalgebra of a direct product that depends fully on all its factors without however necessarily being the whole direct product...
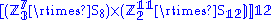, in the notation of Griess.Generalizations
When the centre facet symmetries are taken into account, the symmetry group is a subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of
(This unimportance of centre facet rotations is an implicit example of a quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
at work, shielding the reader from the full automorphism group of the object in question.)
The symmetry group of the Rubik's cube obtained by dismembering it and reassembling is slightly larger: namely it is the direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
The first factor is accounted for solely by rotations of the centre pieces, the second solely by symmetries of the corners, and the third solely by symmetries of the edges. The latter two factors are examples of wreath product
Wreath product
In mathematics, the wreath product of group theory is a specialized product of two groups, based on a semidirect product. Wreath products are an important tool in the classification of permutation groups and also provide a way of constructing interesting examples of groups.Given two groups A and H...
s.
The simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
s that occur as quotients in the composition series
Composition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
of the standard cube group (i.e. ignoring centre piece rotations) are
