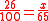Rule of marteloio
Encyclopedia
The rule of marteloio is a medieval
technique of navigation
al computation that uses compass
direction, distance
and a simple trigonometric
table known as the toleta de marteloio. The rule told mariners how to plot the traverse between two different navigation courses
by means of resolving triangle
s with the help of the Toleta and basic arithmetic
.
Those uncomfortable with manipulating numbers could resort to the visual tondo e quadro (circle-and-square) and achieve their answer with dividers. The rule of marteloio was commonly used by Mediterranean navigators during the 14th and 15th centuries, before the development of astronomical navigation
.
comes from the Venetian language
. In his 1436 atlas, Venetian
captain and cartographer Andrea Bianco introduced a table of numbers which he called the toleta de marteloio ("table of marteloio"), and the method of using it as the raxon de marteloio ("reason of marteloio").
The meaning of marteloio itself is uncertain. The most widely accepted hypothesis, first forwarded by A.E. Nordenskiöld
, is that marteloio relates to "hammer
" ("martelo" in Venetian), referring to the small hammer that was used to hit the on-board ship's bell to mark the passage of time. Kelley suggests that the -oio suffix implies that marteloio meant not quite the hammer itself nor the hammerer, but rather "the hammering", intending to indicate "the hammering, the din, the racket" from the change of the watch every four hours. As there were many hands on deck during a change of the watch, it would be an opportune moment for the ship's pilot
to take a speed
reading or order a change in bearing
(if necessary).
Alternative hypotheses (not nearly as accepted) are that "marteloio" is a corruption of mari logio (meaning "rule of the sea"), or from mare tela (meaning "sea network"), or that it derives from the Greek
homartologium (όμαρτόλογίον, meaning "companion piece"), or from the Greek imeralogium (ήμερόλογίον, meaning "daily calculation") or that it might be from the northern French
matelot, which in turn comes from Breton
martolod (meaning "sailors").
, most notably in the Mediterranean Sea
between the 14th and 16th Centuries, although it may have older roots. It was an integral part of navigation by "compass and chart", before the advent of geographical coordinates and the development of celestial navigation
in Europe.
Medieval navigation relied on two parameters, direction and distance. On board ship, direction was determined by the mariner's compass (which emerged around 1300). Distance was measured by dead reckoning
, (i.e., distance = speed × time), where time was measured by a half-hour-glass, and speed readings were taken with by some form of a chip log
(the archaic method, used in the 14th–15th centuries, involved heaving a piece of wood or flotsam overboard; the crew engaged in a rhythmic chant to mark the time it took for the chip to float past the length of the ship).
 Plotting a course required knowing the compass direction and distance between point A and point B. Knowledge of where ports lay relative to each other was acquired by navigators by long experience at sea. This information was sometimes collected and written down in a pilot's handbook, known as a portolano ("port book", in Italian, equivalent to the Greek periplus
Plotting a course required knowing the compass direction and distance between point A and point B. Knowledge of where ports lay relative to each other was acquired by navigators by long experience at sea. This information was sometimes collected and written down in a pilot's handbook, known as a portolano ("port book", in Italian, equivalent to the Greek periplus
, the Portuguese roteiro and the English rutter
). These handbooks were used to construct a class of nautical maps known as portolan charts. Portolan charts began being produced in Genoa
in the late 13th century, and soon spread to Venice
and Majorca. Portolan charts were not gridded by longitude and latitude lines, but rather by a web of compass
rhumb lines, giving mariners an idea of only the distance and direction between places.
By a handbook or a portolan chart, a navigator could see immediately that, for example, Pisa
lay 85 miles southeast ("Scirocco" in the traditional compass rose
nomenclature) of Genoa
, and so a ship that set out from Genoa to Pisa would simply maintain that bearing for that distance. However, most sailing courses were not nearly that neat. A mariner wishing to sail from Majorca to Naples
could tell the latter was due east ("Levante") by some 600 miles – but the island of Sardinia
lies in the way, therefore the ship's bearing must be changed along the route. This is easier said than done, as geographical coordinates did not exist during this era. The only way to determine the exact position of the ship at sea would be to calculate via past bearing and distance travelled.
Islands were a predictable obstacle – circumventing Sardinia would be simply a matter of sailing southeast for a set distance then changing the bearing to northeast ("Greco") for the remainder. More problematic is if the ship were blown off its intended route by fitful winds, or had to engage in tacking
, changing bearing repeatedly. How does it return to its intended course? This is where the rule of marteloio came in.
to another. For example, suppose a ship was to sail from Corsica
to Genoa
, a course bearing straight north ("Tramontana") for some 130 miles. But the winds are not cooperative, and the ship was forced to sail northwest ("Maestro") for some 70 miles. How does it return to its original route? Re-setting its bearing to northeast ("Greco") seems sensible enough, but how long should it sail on that bearing? How would a navigator know when the ship had reached its old route and should turn north again? How to avoid overshooting or undershooting the old course?
This is a mathematical problem of solving a triangle
. If a navigator knows how long the ship has sailed on the erroneous course, he can calculate its current distance from its intended course, and estimate how long it must sail back on a new bearing until it recovers its old course. In the Corsica-to-Genoa example, there is an implied triangle
ACD, with one side given (AC = 70 miles on actual NW course), a 45º angle at A (angle of difference between actual course NW and intended course N) and another angle of 90º at C (angle of difference between actual course NW and return course NE). The challenge to the navigator is to find how long one must sail on the NE return course (the length of side CD, what is called the ritorno) and how far one has advanced on the intended course by the time one straightens out (the length of the hypotenuse AD, or what is called the total avanzo).
This is elementary trigonometry
, solving for two sides given one side (70) and two angles (45º and 90º). This is quickly done by applying the law of sines
:

yielding up the solutions ritorno = 70 miles and total avanzo = 98.99 miles. This means that if the ship bears NE from its current position (C), it will reach its original intended course after 70 miles of sailing on the NE bearing. By the time it reaches its junction point (D), it will have covered 98.99 miles of its original intended course. There it can straighten its bearing N and sail the remaining 30 miles or so to Genoa.
Unfortunately, Medieval sailors with the rudimentary educational levels of the 14th and 15th C., were not likely to know the Law of Sines or manipulate it with ease. As a result, Medieval navigators needed simpler and more accessible method of calculation.
of Majorca, was the first writer to refer to a rule to solve the traverse problem of navigation. In his Arbor Scientiae (1295), in the section of questions on geometry, Llul writes:
What Llull seems to be trying to explain is that a ship actually sailing E, but intending to sail SE, it can figure out how much of its intended southeastward distance it has already made good – what Italians called the "avanzar", but Lull seems to call the "miliaria in mari". Llull does not explain exactly how, but refers only to an "instrument", presumably some sort of trigonometric table. Lull is implying that mariners can calculate the miliaria on the intended course by multiplying the distance actually sailed on the erroneous course by the cosine of the angle between the two routes.
where θ is the angle of difference between the two routes.
Using Lull's example, a ship that intended to sail southeast ("Exaloch" is Catalan
for "Scirocco") but was instead forced to sail east ("Levant"), then the angle of difference is θ = 45º. After 100 miles on the erroneous route, the miliaria on the intended route is 100 × cos 45º = 70.71. Doubling the sailing on the erroneous route to 200 miles will double the miliaria on the intended route to 141.42 miles (= 200 cos 45º).
(Diagramatically, Lull's miliaria in mari is measured by constructing a right-angled triangle by running a cord from the distance sailed on the actual course to the intended course, meeting the latter at a 90º angle).
Llull is a little more explicit in his Ars magna generalis et ultima (written c.1305). Reversing his example, with a ship actually sailing Southeast but intending to sail East, Llull notes that for every four miles on the southeast bearing, it gains three miles (2.83 actually) on the intended eastward route. Thus, Lull notes, the ship "loses 25 miles" (29 actually) of its intended course for every 100 miles it sails on the current course.
Notice that in his passages, Ramon Lull is not recommending the rule, but reporting it, insinuating that this rule was already known and used by contemporary sailors in practice. This is perhaps unsurprising – although trigonometry was only in its infancy in Christian Europe, sine and cosine tables were already known in Arab mathematics. The Kingdom of Majorca
, under Muslim rule until the 1230s, remained a multicultural center in Lull's time, with flourishing Muslim and Jewish communities, many of whom dabbled in mathematics and astronomy, and whose seafarers had extensive contact across the Mediterranean Sea. That Majorcan navigators had some sort of trigonometric table at hand is not improbable. Nonetheless, the exact content and layout of this table implied by Ramon Llull in 1295 is uncertain.
, the Venetian
captain Andrea Bianco explains the raxon de marteloio, how to calculate the traverse and recover the course. He lays out a simple trigonometric table he calls the toleta de marteloio and recommends that mariners commit the table to memory.
The toleta de marteloio is set out as follows:
The numbers in the Toleta can be approximated by the modern formulas:
where q = number of quarter winds (angle of difference expressed in number of quarter winds). (notice that the numbers work with quarter-winds set at 11.15º intervals, rather than 11.25º, the usual definition of a quarter wind).
The Toleta is a simple table with several columns of numbers. In the first column is the angle of difference between the actual and intended courses, expressed by number of quarter-winds. Once that difference is determined, the second column gives the Alargar (the "Widening", the current distance the ship is from the intended course) while the third column tells the Avanzar (the "Advance", how much of the distance on the intended course has already been covered by sailing on the current bearing – this is equivalent of Ramon Llull's miliaria di mari). The Alargar and Avanzar numbers are shown on the Bianco's table for 100 miles of sailing on the current course.
Example: suppose a ship intended to sail bearing east ("Levante") from point A to point B. But suppose that winds forced it to sail on a southeast-by-east course (SEbE, "Quarto di Scirocco verso Levante"). Southeast-by-east is three quarter winds (or 33.75°) away from east (on a 32-point compass
, in order of quarter-winds away from east, 1 quarter is east-by-south, 2 quarters is East-southeast, 3 quarters is southeast-by-east). That means that the navigator should consult the third row, q = 3, on the toleta.
Suppose the ship sailed 100 miles on the SE-by-E bearing. To check his distance from the intended eastward course, the mariner will read the corresponding entry on the alargar column and immediately see he is 55 miles away from the intended course. The avanzar column informs him that having sailed 100 miles on the current SEbE course, he has covered 83 miles of the intended E course.
The next step is to determine how to return to the intended course. Continuing the example, to get back to the intended Eastward course, our mariner has to re-orient the ship's bearing in a northeasterly direction. But there are various northeasterly angles – NbE, NNE, NE, ENE, etc. The mariner has a choose the bearing – if he returns by a sharp angle (e.g. North by east), he will return to the intended course faster than at a more gentle gradient (e.g. East by north). Whichever angle he chooses, he must deduce exactly how long he must sail on that bearing in order to reach his old course. If he sails too long, he risks overshooting it.
This is what the third column of the toleta is for. The return angles are expressed as quarters from the intended course bearing (not the current course bearing). In our example, the mariner intended to go east, but has been sailing southeast-by-east for 100 miles. Given the winds, he decides it is best to return to the original course by re-orienting the ship east-northeast (ENE, "Greco-Levante"). ENE is two quarter-winds above the intended bearing, East, so now he looks at second row ("quarters = 2") on the table. In the third column, the ritorno, shows the number 26. This represents the required number of miles he must travel on ENE bearing for every 10 miles of alargar. Remember, his alargar (distance from intended course) was 55 miles. So in order to return to his intended course he must travel 5.5 × 26 = 143 miles on ENE. In other words, he needs to hold his ENE bearing for 143 miles; once that distance is travelled, he should straighten his ship East, and he will be exactly on the intended course.
The final column (avanzo di ritorno) gives the length on the intended course he has made good by his return travel. This is also expressed in terms per 10 miles alargar. His alargar was 55, and his angle of return was ENE (thus q = 2), that means his avanzo di ritorno is 5.5 × 24 = 132. In other words, if everything goes right, and our mariner holds his ENE bearing for 143 miles (ritorno), then during that return, he will have covered an additional 132 miles on his intended eastward course (avanzo di ritorno).
Finally, the total avanzo on the eastward bearing is the avanzar during the deviation (83 miles) plus the avanzo di ritorno (132 miles), thus on the whole, he has covered 83 + 132 = 215 miles on the intended course. Measuring that distance on the map from the starting point (A), the mariner can figure out his exact current position.
This is the simplest use of the toleta de marteloio. It is, at root, a trigonometric table. However,it does not tackle the traverse problem in one go, like the Law of Sines, but rather splits the problem into two right-angled triangles which it proceeds to solve successively. Modern trigonometry
would dispense with the step of calculating the alargar, and calculate the ritorno directly – but for that, one needs to be armed with a full sine table. The toleta is a rather simple table, easy to consult and perform calculations with, and sufficiently compact to be memorized by navigators (as Bianco recommends).
s. For example, if the ship had sailed 65 miles on southeast-by-east, then calculating the alargar from the intended Eastward course is simply a matter of solving the following for :
where 26 is the alargar for 100 miles (as given in the second column of the table). This is easily done by the simple "Rule of Three", a method of cross-multiplication, using three numbers to solve for the fourth by successive multiplication and division:
So, sailing for 65 miles on SE by E implies alargar = = 16.9 miles. The avanzar, etc. can be figured out analogously.
While the "rule of three" was already known in the 14th C., skill in executing multiplication
and division
could be elusive for Medieval sailors drawn from what was a largely illiterate society. Nonetheless, it was not inaccessible. As Andrea Bianco urged, navigators should "know how to multiply well and divide well" ("saver ben moltiplichar e ben partir") It is here where we see the important interface of commerce
and navigation. The mathematics of commerce – Arabic numerals
, multiplication, division, fractions
, the tools needed to calculate purchases and sales of goods and other commercial transactions – was essentially the same as the mathematics of navigation. And this kind of mathematics was taught at the abacus school
s which were set up in the 13th C. in the commercial centers of northern Italy to train the sons of merchants, the very same class where Italian navigators were drawn from. As historian E.G.R. Taylor notes, "sailors were the first professional group to use mathematics in their everyday work"
The circle was a 32-wind compass rose
(or gathering of rhumb-lines). The circle was inscribed with a 8 × 8 square grid.
The compass rose in the center can be overlooked – indeed, the circle itself can be ignored, as it is seems to have no other purpose than the construction of the rays that run across the grid. The rose of interest is in the upper left corner of the square grid. From that corner, emanate a series of compass rhumb lines. In his original 1436 tondo e quadro, Bianco has sixteen emanating rays – that is, Bianco includes half-quarter winds, or eighth-winds (otava), so that the emanating rays are at intervals of 5.625 degrees. Other constructions of the circle-and-square, e.g. the Cornaro Atlas
, use only eight rays emanating at quarter-wind distances (11.25 degrees). Visually, these rays replicate the bottom right quarter of a 32-wind compass rose
: East (0q), E by S (1q), ESE (2q), SE by E (3q), SE (4q), SE by S (5q), SSE (6q), S by E (7q) and South (8q).
Above the grid is a distance bar scale
, notched with sub-units. There are two sets of numbers on the scale, one for measuring each grid square by 20 miles, another for measuring each grid square by 100 miles (see diagram). The top bar is the 20m-per-square scale, with every black dot denoting one mile. The bottom bar is the 100m-per-square scale, where the length of a unit square is divided into two equal 50m sub-squares, and a set of dots and red lines break it down further into lengths of 10 miles. So depending on which scale one chooses, the length of the side of the entire grid (eight squares) could be measured up to 160 miles (using the 20m-per-square scale) or up to 800 miles (using the 100m-per-square scale).
The cherub with the dividers suggests how a navigator is supposed to use the grid to calculate alargar and avanzar by visual measurement rather than manipulating numbers.
Example: suppose the ship has travelled 120 miles at two quarter-winds below the intended course (e.g. traveled at ESE, when the intended course is East). Using the dividers and the 20m scale, the navigator can measure out 120 miles with his dividers. Then setting one end at the top left corner (A), he lays out the dividers along the ESE ray (= two quarter-winds below the East ray, or horizontal top of the grid) and marks the spot (point B on the diagram). Then using a straightedge
ruler draws a line up to the East ray, and marks the corresponding spot C.
It is easy to see immediately that a right-angled triangle ABC has been created. The length BC is the alargar (distance from intended course), which can be measured as 46 miles (this can be visually seen as two grid squares plus a bit, that is 20m + 20m and a little bit which can be assessed as 6m by using the dividers and the 20m bar scale). The length AC is the avanzar (distance made good), which is 111 miles – visually, five grid squares and a bit, or (20 × 5) + 11, measured by dividers and scale again.
This is how the "circle and square" dispenses manipulating numbers by multiplication and division or the rule of three. The navigator can assess the avanzar and alargar visually, by measurement alone.
This method can be used for any intended bearing and deviation, as the only purpose is to solve the triangle by dividers and scale. e.g. using our first Corsica-to-Genoa example, where intended bearing was North but the ship actually sailed Northwest, the navigator would set the dividers at length 70 miles and lay it along the fourth quarter wind (= SE ray in the tondo e quadro, as NW is four quarter winds away from North). He would calculate the alargar and avanzar in exactly the same way – draw a line to the horizontal top of the grid, measure the squares, etc.
The tondo e quadro device is very similar to the Arab sine quadrant (Rubul mujayyab), with the corner rays replicating the role of the adjustable plumb line.
, e.g. determining the distance of the ship from shore landmark. (This was the final exercise attempted by Michael of Rhodes, which we replicate here with slightly different numbers.)
Example: Suppose a ship sailing NW ("Maestro") spots a landmark due West ("Ponente") one evening, but distance unknown. Suppose the ship continues sailing on the NW route overnight, and the next morning, 40 miles later, it notices that landmark is now west-southwest (WSW, "Ponente-Libeccio") of its current position. Finding the distance of the landmark from the ship is just an application of the rule of marteloio.
To solve the problem, start from the evening position (A on the map) and treat the distance between the ship and the landmark (length AB) as the intended course, and the actual route of the ship (NW) as a deviation. To figure out the distance of the landmark from the ship's position in the morning (C) is a matter of treating the distance BC as the calculated ritorno. Since we need to know the alargar to calculate the ritorno, this is a two-step procedure.
First, notice that NW is four quarter-winds above W, so looking up on the toleta, in the q = 4 row, the alargar is 71 miles for every 100 miles on the NW course. But the ship only sailed 40 miles overnight, so we have to solve the ratio 71/100 = x/40, which by the rule of three
means x = alargar = 28.4 miles. In other words, by the overnight sailing NW by 40 miles from A to C, the ship is now 28.4 miles away from its "intended" Westward course.
Now for the ritorno. The landmark, as noted, is WSW of the ship's morning position (C). So to "return" to the landmark, the ship must change its bearing from its current NW bearing to a WSW bearing – that is, 6 quarter-winds below NW. However, the toleta specifies quarter winds in terms of "intended" direction (in this case, West), and WSW is two quarter winds below West, so we need to look at the q = 2 row. This means the ritorno is 26 miles for every 10 miles alargar. Since the alargar is 28.4, that means the ritorno is 26 × 2.84 = 73.84. And there we have it. The landmark is 73.84 miles away from the ship's morning position.
(To complete the story, we might wish to find out the distance that landmark was the evening before (i.e. from point A to landmark B). That is simply a matter of adding the avanzar and the avanzo in ritorno. Quick calculations show the avanzar (@ q = 4, for 40 miles) is 28.4 miles (= 71 × 40/100) and the avanzo di ritorno (@ q = 2 for 28.4 miles alargar), is 2.84 × 24 = 68.16. So total avanzo = 28.4 + 68.16 = 96.56 miles. That was the distance between the landmark and the ship the evening before.)
legally set in a 1494 treaty at 370 leagues west of Cape Verde
. The ship need not set out from Cape Verde and set sail constantly at West bearing to find it. Rather, it can sail out at a more convenient bearing (e.g. SW), and treat West as an "intended" course. So using the marteloio rule, it can sail on until the avanzar on the "intended" West course reaches 370 leagues.
Indeed it need not even set out from Cape Verde, but can set out from another place, say, Seville
, and use the known distance and bearing of Cape Verde (viz. Seville) and the rule of marteloio to calculate when it has finally reached the Tordesillas meridian. This takes a couple of steps. Suppose Cape Verde (B on map) is 400 leagues Southwest of Seville (A on map), but the ship intends to go straight West from Seville to reach the Tordesillas meridian in the open sea. How long does it need to sail?
The way to solve this by the rule of marteloio is to pose the problem in reverse: treat West as intended bearing and SW as the actual course. SW is four quarter-winds below W, so looking up the toleta for q = 4, the avanzar is 71 for every 100 miles sailed. So if a ship sailed 400 leagues on the "actual" SW course to Cape Verde, it would achieve an avanzar of 284 leagues (= 71 × 4) on the "intended" Westward course. Of course, the ship is not actually sailing SW to Cape Verde, but sailing W into the open sea. In other words, when the ship sets sail West from Seville, it knows it needs to sail 284 leagues on the West bearing before it reaches the implied Cape Verde meridian
(point C on map), and should only start counting the 370 leagues to the Tordesillas line thereafter. In other words, it needs to sail a total of 284 + 370 = 654 leagues West of Seville to reach the Tordesillas line (point D on map).
While this particular example shows the flexibility of the rule of marteloio, it also shows one of its principal drawbacks: the result completely ignores the curvature of the earth, i.e. the fact that the longitude
meridian lines converge on the North Pole
, and thus narrow at higher latitudes. Contrary to what the marteloio suggests, 370 leagues West of Cape Verde is not on the same longitude meridian as 654 leagues West of Seville. Because Seville is well north of Cape Verde, the meridians are clustered closer together at Seville's latitude than at Cape Verde's latitude. A ship sailing west of Seville will, in fact, reach the real Tordesillas meridian (point T on map) well before 654 leagues are sailed (point D).
The rule of marteloio has sailors plot routes by drawing plane triangles on a chart, as if the world's surface were flat. While this might be practical enough for sailing confined to the compact latitudes of the Mediterranean Sea
, it is quite misleading on a grander scale.
and the introduction of latitude
parallels allowed navigators to determine their position at sea by celestial readings, rather than relying on estimation of distance sailed. The successor of the rule of marteloio was the "Regiment of the Leagues" (regimento das léguas), that was used by Portuguese navigators sailing in the Atlantic Ocean. Or, to use the term introduced by William Bourne
(1571), the "Rule to Raise or Lay a Degree", also known as the "Table of Leagues" or the "Rule for Raising the Pole". It was first written down in the Portuguese
navigation manual Regimento do astrolabio e do quadrante (published in Lisbon c.1509, but written c.1480) It was popularized by Martín Cortés de Albacar
in his 1551 Breve compendio la esfera y del arte de navegar.
The "Regiment of the Leagues" is not very different from the rule of marteloio. The Regiment of the Leagues always considers the west-east bearing as the "intended course" and measures set deviations from it. More specifically, the league table considers a fixed value of alargar – set at 1 latitude degree (or, in the measurements of the time, 17.5 (Portuguese) leagues
, or equivalently 70 (Italian) miles
). It then gives for every different quarter wind of sailing direction (always designated as quarters away from the north-south axis, rather than away from the intended course), the relevar and the afastar. The relevar is the number of leagues on the actual course that a ship must sail in order to cover the pre-set 1 degree of latitude (17.5 leagues of alargar from the starting parallel). The afastar is merely the corresponding avanzar on the west-east bearing.
Example: Suppose a ship sets out on an East-southeast (ESE) bearing. That is six quarter-winds above South (remember: unlike the marteloio, the Regiment of the Leagues always measures quarter-winds away from the north–south meridian). Looking at any regiment of the leagues table (e.g. Martín Cortés de Albacar
, 1551), for q = 6, the table gives the relevar as 45 leagues and the afastar as 42 leagues. This means that a ship sailing on the ESE bearing will have to sail 45.73 leagues to cover one degree of latitude (17.5 leagues of alargar from the east bearing, to use the marteloio language), and the corresponding afastar (avanzar in marteloio terms) will be 42.25 leagues.
If, instead, the ship had set out on a SE bearing, that is four quarter-winds above South, the corresponding values of the Regiment of the Leagues table at q = 4 are relevar = 24 and the afastar = 17 .
Notice that the SE bearing reaches the 1 degree alargar faster (i.e. smaller relevar) than that the ESE bearing, and will have less afastar (closer to the N–S meridian).
Mathematically,
where θ = 11.25 × number of quarters-winds away from the north-south axis.
Despite the difference in terminology, notably the use of latitude degrees, the rule of marteloio and the Regiment of the Leagues are very similar – they are both about solving triangles on a plane chart. The advantage of the regiment over the marteloio is the introduction of latitude parallels in the table, so that the position can be checked by astronomical observation (via quadrant
, astrolabe
, etc.), and not have to rely wholly on sailor estimations of distance and direction.
With the regiment, geographical coordinates can also be used to guide navigation. For instance, the search for the Todesillas line (meridian 370 leagues west of Cape Verde) is much simplified by reference to a precise latitude. For instance, suppose two ships depart from Cape Verde (17° N), one on an West by North bearing (WbN, that is one quarter above West, or q = 7 from North axis), the other by a west-northwest bearing (WNW, two quarters above west, or q = 6 from the North axis). Using the Regiment of the Leagues, it is possible to calculate the precise latitudes when they will cross the Tordesillas meridian – simply divide 370 leagues west by the implied afastar at the different bearings. The WbN ship will reach the meridian when it achieves latitude 21° 21' N, while the WNW ship will reach it when it achieves latitude 29° N. So rather than counting leagues with hourglass and speed readings, the ships can just maintain bearing, and take periodic astronomical observations to assess their latitude.
Traverse tables use three values for each of the crooked course segments – the Distance (Dist.), Difference of Latitude (D.Lat., movement along N–S axis) and the Departure (Dep., movement along E–W axis), the latter two calculated by the formulas:
where θ is the angular difference of the course from the N–S axis if the values of θ are less than 45°; if, however, the angle exceeds 45°, then θ is expressed as the angle of difference from the E–W axis, and the formulas are flipped, i.e. Difference of Latitude formula becomes the Departure, and the Departure formula is the Difference of Latitude). Or, even more simply, calculate θ as the angle of difference from the nearest principal wind (N, S, E, W), run the formulas and then place the larger number in the appropriate column (D.Lat. or Dep.).
For each course segment, the navigator inserts the relevant trio (Dist., D.Lat., Dep.) and can calculate the implied bearing from the beginning to the endpoint and the distance made good on that bearing. He then combines, by addition and substraction, all the differences of latitude and departure, to get the overall difference of latitude and departure, and converts that back to overall bearing and distance made good.
's suggestive 1295 remarks aside, the earliest known reference to marteloio is dated 1390, in the inventory of the estate of the mother of a certain Oberto Foglieto of Genoa, where an entry reads unum martelogium....item carta una pro navegando. The first clear appearance and explanation is the 1436 atlas of Venetian captain Andrea Bianco. Other early manuscripts have since been found relating the rule of marteloio, incude:
Middle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
technique of navigation
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
al computation that uses compass
Compass
A compass is a navigational instrument that shows directions in a frame of reference that is stationary relative to the surface of the earth. The frame of reference defines the four cardinal directions – north, south, east, and west. Intermediate directions are also defined...
direction, distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
and a simple trigonometric
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
table known as the toleta de marteloio. The rule told mariners how to plot the traverse between two different navigation courses
Course (navigation)
In navigation, a vehicle's course is the angle that the intended path of the vehicle makes with a fixed reference object . Typically course is measured in degrees from 0° clockwise to 360° in compass convention . Course is customarily expressed in three digits, using preliminary zeros if needed,...
by means of resolving triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s with the help of the Toleta and basic arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
.
Those uncomfortable with manipulating numbers could resort to the visual tondo e quadro (circle-and-square) and achieve their answer with dividers. The rule of marteloio was commonly used by Mediterranean navigators during the 14th and 15th centuries, before the development of astronomical navigation
Celestial navigation
Celestial navigation, also known as astronavigation, is a position fixing technique that has evolved over several thousand years to help sailors cross oceans without having to rely on estimated calculations, or dead reckoning, to know their position...
.
Etymology
The etymologyEtymology
Etymology is the study of the history of words, their origins, and how their form and meaning have changed over time.For languages with a long written history, etymologists make use of texts in these languages and texts about the languages to gather knowledge about how words were used during...
comes from the Venetian language
Venetian language
Venetian or Venetan is a Romance language spoken as a native language by over two million people, mostly in the Veneto region of Italy, where of five million inhabitants almost all can understand it. It is sometimes spoken and often well understood outside Veneto, in Trentino, Friuli, Venezia...
. In his 1436 atlas, Venetian
Venice
Venice is a city in northern Italy which is renowned for the beauty of its setting, its architecture and its artworks. It is the capital of the Veneto region...
captain and cartographer Andrea Bianco introduced a table of numbers which he called the toleta de marteloio ("table of marteloio"), and the method of using it as the raxon de marteloio ("reason of marteloio").
The meaning of marteloio itself is uncertain. The most widely accepted hypothesis, first forwarded by A.E. Nordenskiöld
Adolf Erik Nordenskiöld
Freiherr Nils Adolf Erik Nordenskiöld , also known as A. E. Nordenskioeld was a Finnish baron, geologist, mineralogist and arctic explorer of Finnish-Swedish origin. He was a member of the prominent Finland-Swedish Nordenskiöld family of scientists...
, is that marteloio relates to "hammer
Hammer
A hammer is a tool meant to deliver an impact to an object. The most common uses are for driving nails, fitting parts, forging metal and breaking up objects. Hammers are often designed for a specific purpose, and vary widely in their shape and structure. The usual features are a handle and a head,...
" ("martelo" in Venetian), referring to the small hammer that was used to hit the on-board ship's bell to mark the passage of time. Kelley suggests that the -oio suffix implies that marteloio meant not quite the hammer itself nor the hammerer, but rather "the hammering", intending to indicate "the hammering, the din, the racket" from the change of the watch every four hours. As there were many hands on deck during a change of the watch, it would be an opportune moment for the ship's pilot
Maritime pilot
A pilot is a mariner who guides ships through dangerous or congested waters, such as harbours or river mouths. With the exception of the Panama Canal, the pilot is only an advisor, as the captain remains in legal, overriding command of the vessel....
to take a speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
reading or order a change in bearing
Bearing (navigation)
In marine navigation, a bearing is the direction one object is from another object, usually, the direction of an object from one's own vessel. In aircraft navigation, a bearing is the actual compass direction of the forward course of the aircraft...
(if necessary).
Alternative hypotheses (not nearly as accepted) are that "marteloio" is a corruption of mari logio (meaning "rule of the sea"), or from mare tela (meaning "sea network"), or that it derives from the Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
homartologium (όμαρτόλογίον, meaning "companion piece"), or from the Greek imeralogium (ήμερόλογίον, meaning "daily calculation") or that it might be from the northern French
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
matelot, which in turn comes from Breton
Breton language
Breton is a Celtic language spoken in Brittany , France. Breton is a Brythonic language, descended from the Celtic British language brought from Great Britain to Armorica by migrating Britons during the Early Middle Ages. Like the other Brythonic languages, Welsh and Cornish, it is classified as...
martolod (meaning "sailors").
Purpose
The "rule of marteloio" was used in European navigation in the Middle AgesMiddle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
, most notably in the Mediterranean Sea
Mediterranean Sea
The Mediterranean Sea is a sea connected to the Atlantic Ocean surrounded by the Mediterranean region and almost completely enclosed by land: on the north by Anatolia and Europe, on the south by North Africa, and on the east by the Levant...
between the 14th and 16th Centuries, although it may have older roots. It was an integral part of navigation by "compass and chart", before the advent of geographical coordinates and the development of celestial navigation
Celestial navigation
Celestial navigation, also known as astronavigation, is a position fixing technique that has evolved over several thousand years to help sailors cross oceans without having to rely on estimated calculations, or dead reckoning, to know their position...
in Europe.
Medieval navigation relied on two parameters, direction and distance. On board ship, direction was determined by the mariner's compass (which emerged around 1300). Distance was measured by dead reckoning
Dead reckoning
In navigation, dead reckoning is the process of calculating one's current position by using a previously determined position, or fix, and advancing that position based upon known or estimated speeds over elapsed time, and course...
, (i.e., distance = speed × time), where time was measured by a half-hour-glass, and speed readings were taken with by some form of a chip log
Chip log
A chip log, also called common log, ship log or just log, is a navigation tool used by mariners to estimate the speed of a vessel through water.-Construction:...
(the archaic method, used in the 14th–15th centuries, involved heaving a piece of wood or flotsam overboard; the crew engaged in a rhythmic chant to mark the time it took for the chip to float past the length of the ship).

Periplus
Periplus is the Latinization of an ancient Greek word, περίπλους , literally "a sailing-around." Both segments, peri- and -plous, were independently productive: the ancient Greek speaker understood the word in its literal sense; however, it developed a few specialized meanings, one of which became...
, the Portuguese roteiro and the English rutter
Rutter (nautical)
A rutter is a mariner's handbook of written sailing directions. Before the advent of nautical charts, rutters were the primary store of geographic information for maritime navigation....
). These handbooks were used to construct a class of nautical maps known as portolan charts. Portolan charts began being produced in Genoa
Genoa
Genoa |Ligurian]] Zena ; Latin and, archaically, English Genua) is a city and an important seaport in northern Italy, the capital of the Province of Genoa and of the region of Liguria....
in the late 13th century, and soon spread to Venice
Venice
Venice is a city in northern Italy which is renowned for the beauty of its setting, its architecture and its artworks. It is the capital of the Veneto region...
and Majorca. Portolan charts were not gridded by longitude and latitude lines, but rather by a web of compass
Compass rose
A compass rose, sometimes called a windrose, is a figure on a compass, map, nautical chart or monument used to display the orientation of the cardinal directions — North, East, South and West - and their intermediate points. It is also the term for the graduated markings found on the traditional...
rhumb lines, giving mariners an idea of only the distance and direction between places.
By a handbook or a portolan chart, a navigator could see immediately that, for example, Pisa
Pisa
Pisa is a city in Tuscany, Central Italy, on the right bank of the mouth of the River Arno on the Tyrrhenian Sea. It is the capital city of the Province of Pisa...
lay 85 miles southeast ("Scirocco" in the traditional compass rose
Compass rose
A compass rose, sometimes called a windrose, is a figure on a compass, map, nautical chart or monument used to display the orientation of the cardinal directions — North, East, South and West - and their intermediate points. It is also the term for the graduated markings found on the traditional...
nomenclature) of Genoa
Genoa
Genoa |Ligurian]] Zena ; Latin and, archaically, English Genua) is a city and an important seaport in northern Italy, the capital of the Province of Genoa and of the region of Liguria....
, and so a ship that set out from Genoa to Pisa would simply maintain that bearing for that distance. However, most sailing courses were not nearly that neat. A mariner wishing to sail from Majorca to Naples
Naples
Naples is a city in Southern Italy, situated on the country's west coast by the Gulf of Naples. Lying between two notable volcanic regions, Mount Vesuvius and the Phlegraean Fields, it is the capital of the region of Campania and of the province of Naples...
could tell the latter was due east ("Levante") by some 600 miles – but the island of Sardinia
Sardinia
Sardinia is the second-largest island in the Mediterranean Sea . It is an autonomous region of Italy, and the nearest land masses are the French island of Corsica, the Italian Peninsula, Sicily, Tunisia and the Spanish Balearic Islands.The name Sardinia is from the pre-Roman noun *sard[],...
lies in the way, therefore the ship's bearing must be changed along the route. This is easier said than done, as geographical coordinates did not exist during this era. The only way to determine the exact position of the ship at sea would be to calculate via past bearing and distance travelled.
Islands were a predictable obstacle – circumventing Sardinia would be simply a matter of sailing southeast for a set distance then changing the bearing to northeast ("Greco") for the remainder. More problematic is if the ship were blown off its intended route by fitful winds, or had to engage in tacking
Tacking (sailing)
Tacking or coming about is a sailing maneuver by which a sailing vessel turns its bow through the wind so that the direction from which the wind blows changes from one side to the other...
, changing bearing repeatedly. How does it return to its intended course? This is where the rule of marteloio came in.
The traverse problem
The rule of marteloio addressed the problem of changing bearing at sea. More specifically, it helped a navigator plot the traverse from one navigational courseCourse (navigation)
In navigation, a vehicle's course is the angle that the intended path of the vehicle makes with a fixed reference object . Typically course is measured in degrees from 0° clockwise to 360° in compass convention . Course is customarily expressed in three digits, using preliminary zeros if needed,...
to another. For example, suppose a ship was to sail from Corsica
Corsica
Corsica is an island in the Mediterranean Sea. It is located west of Italy, southeast of the French mainland, and north of the island of Sardinia....
to Genoa
Genoa
Genoa |Ligurian]] Zena ; Latin and, archaically, English Genua) is a city and an important seaport in northern Italy, the capital of the Province of Genoa and of the region of Liguria....
, a course bearing straight north ("Tramontana") for some 130 miles. But the winds are not cooperative, and the ship was forced to sail northwest ("Maestro") for some 70 miles. How does it return to its original route? Re-setting its bearing to northeast ("Greco") seems sensible enough, but how long should it sail on that bearing? How would a navigator know when the ship had reached its old route and should turn north again? How to avoid overshooting or undershooting the old course?
This is a mathematical problem of solving a triangle
Solution of triangles
In trigonometry, to solve a triangle is to find the three angles and the lengths of the three sides of the triangle when given some, but not all of that information...
. If a navigator knows how long the ship has sailed on the erroneous course, he can calculate its current distance from its intended course, and estimate how long it must sail back on a new bearing until it recovers its old course. In the Corsica-to-Genoa example, there is an implied triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
ACD, with one side given (AC = 70 miles on actual NW course), a 45º angle at A (angle of difference between actual course NW and intended course N) and another angle of 90º at C (angle of difference between actual course NW and return course NE). The challenge to the navigator is to find how long one must sail on the NE return course (the length of side CD, what is called the ritorno) and how far one has advanced on the intended course by the time one straightens out (the length of the hypotenuse AD, or what is called the total avanzo).
This is elementary trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, solving for two sides given one side (70) and two angles (45º and 90º). This is quickly done by applying the law of sines
Law of sines
In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
:

yielding up the solutions ritorno = 70 miles and total avanzo = 98.99 miles. This means that if the ship bears NE from its current position (C), it will reach its original intended course after 70 miles of sailing on the NE bearing. By the time it reaches its junction point (D), it will have covered 98.99 miles of its original intended course. There it can straighten its bearing N and sail the remaining 30 miles or so to Genoa.
Unfortunately, Medieval sailors with the rudimentary educational levels of the 14th and 15th C., were not likely to know the Law of Sines or manipulate it with ease. As a result, Medieval navigators needed simpler and more accessible method of calculation.
Ramon Llull's "miliaria"
The scholar-cleric Ramon LlullRamon Llull
Ramon Llull was a Majorcan writer and philosopher, logician and tertiary Franciscan. He wrote the first major work of Catalan literature. Recently-surfaced manuscripts show him to have anticipated by several centuries prominent work on elections theory...
of Majorca, was the first writer to refer to a rule to solve the traverse problem of navigation. In his Arbor Scientiae (1295), in the section of questions on geometry, Llul writes:
What Llull seems to be trying to explain is that a ship actually sailing E, but intending to sail SE, it can figure out how much of its intended southeastward distance it has already made good – what Italians called the "avanzar", but Lull seems to call the "miliaria in mari". Llull does not explain exactly how, but refers only to an "instrument", presumably some sort of trigonometric table. Lull is implying that mariners can calculate the miliaria on the intended course by multiplying the distance actually sailed on the erroneous course by the cosine of the angle between the two routes.
- Miliaria in mari = distance sailed × cos(θ)
where θ is the angle of difference between the two routes.
Using Lull's example, a ship that intended to sail southeast ("Exaloch" is Catalan
Catalan language
Catalan is a Romance language, the national and only official language of Andorra and a co-official language in the Spanish autonomous communities of Catalonia, the Balearic Islands and Valencian Community, where it is known as Valencian , as well as in the city of Alghero, on the Italian island...
for "Scirocco") but was instead forced to sail east ("Levant"), then the angle of difference is θ = 45º. After 100 miles on the erroneous route, the miliaria on the intended route is 100 × cos 45º = 70.71. Doubling the sailing on the erroneous route to 200 miles will double the miliaria on the intended route to 141.42 miles (= 200 cos 45º).
(Diagramatically, Lull's miliaria in mari is measured by constructing a right-angled triangle by running a cord from the distance sailed on the actual course to the intended course, meeting the latter at a 90º angle).
Llull is a little more explicit in his Ars magna generalis et ultima (written c.1305). Reversing his example, with a ship actually sailing Southeast but intending to sail East, Llull notes that for every four miles on the southeast bearing, it gains three miles (2.83 actually) on the intended eastward route. Thus, Lull notes, the ship "loses 25 miles" (29 actually) of its intended course for every 100 miles it sails on the current course.
Notice that in his passages, Ramon Lull is not recommending the rule, but reporting it, insinuating that this rule was already known and used by contemporary sailors in practice. This is perhaps unsurprising – although trigonometry was only in its infancy in Christian Europe, sine and cosine tables were already known in Arab mathematics. The Kingdom of Majorca
Kingdom of Majorca
The Kingdom of Majorca was founded by James I of Aragon, also known as James The Conqueror. After the death of his first-born son Alfonso, a will was written in 1262 which created the kingdom in order to cede it to his son James...
, under Muslim rule until the 1230s, remained a multicultural center in Lull's time, with flourishing Muslim and Jewish communities, many of whom dabbled in mathematics and astronomy, and whose seafarers had extensive contact across the Mediterranean Sea. That Majorcan navigators had some sort of trigonometric table at hand is not improbable. Nonetheless, the exact content and layout of this table implied by Ramon Llull in 1295 is uncertain.
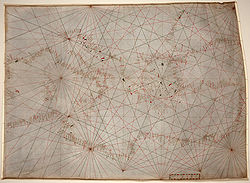
Andrea Bianco's "toleta"
We get our first glimpse of a mariner's trigonometric table more than a century after Llull. In the first folio of his 1436 portolan atlasPortolan chart
Portolan charts are navigational maps based on realistic descriptions of harbours and coasts. They were first made in the 14th century in Italy, Portugal and Spain...
, the Venetian
Venice
Venice is a city in northern Italy which is renowned for the beauty of its setting, its architecture and its artworks. It is the capital of the Veneto region...
captain Andrea Bianco explains the raxon de marteloio, how to calculate the traverse and recover the course. He lays out a simple trigonometric table he calls the toleta de marteloio and recommends that mariners commit the table to memory.
The toleta de marteloio is set out as follows:
| Quarter | Alargar (Distance from course) |
Avanzar (Advance on true course) |
Ritorno (Return to course) |
Avanzo di ritorno (Advance during return) |
|---|---|---|---|---|
| 1 | 20 | 98 | 51 | 50 |
| 2 | 38 | 92 | 26 | 24 |
| 3 | 55 | 83 | 18 | 15 |
| 4 | 71 | 71 | 14 | 10 |
| 5 | 83 | 55 | 12 | 6 |
| 6 | 92 | 38 | 11 | 4 |
| 7 | 98 | 20 | 10 | 2 |
| 8 | 100 | 0 | 10 | 0 |
| For every 10 miles alargar | ||||
The numbers in the Toleta can be approximated by the modern formulas:
- Alargar =
- Avanzar =
- Ritorno =
- Avanzo di ritorno =
where q = number of quarter winds (angle of difference expressed in number of quarter winds). (notice that the numbers work with quarter-winds set at 11.15º intervals, rather than 11.25º, the usual definition of a quarter wind).
The Toleta is a simple table with several columns of numbers. In the first column is the angle of difference between the actual and intended courses, expressed by number of quarter-winds. Once that difference is determined, the second column gives the Alargar (the "Widening", the current distance the ship is from the intended course) while the third column tells the Avanzar (the "Advance", how much of the distance on the intended course has already been covered by sailing on the current bearing – this is equivalent of Ramon Llull's miliaria di mari). The Alargar and Avanzar numbers are shown on the Bianco's table for 100 miles of sailing on the current course.
Example: suppose a ship intended to sail bearing east ("Levante") from point A to point B. But suppose that winds forced it to sail on a southeast-by-east course (SEbE, "Quarto di Scirocco verso Levante"). Southeast-by-east is three quarter winds (or 33.75°) away from east (on a 32-point compass
Compass rose
A compass rose, sometimes called a windrose, is a figure on a compass, map, nautical chart or monument used to display the orientation of the cardinal directions — North, East, South and West - and their intermediate points. It is also the term for the graduated markings found on the traditional...
, in order of quarter-winds away from east, 1 quarter is east-by-south, 2 quarters is East-southeast, 3 quarters is southeast-by-east). That means that the navigator should consult the third row, q = 3, on the toleta.
Suppose the ship sailed 100 miles on the SE-by-E bearing. To check his distance from the intended eastward course, the mariner will read the corresponding entry on the alargar column and immediately see he is 55 miles away from the intended course. The avanzar column informs him that having sailed 100 miles on the current SEbE course, he has covered 83 miles of the intended E course.
The next step is to determine how to return to the intended course. Continuing the example, to get back to the intended Eastward course, our mariner has to re-orient the ship's bearing in a northeasterly direction. But there are various northeasterly angles – NbE, NNE, NE, ENE, etc. The mariner has a choose the bearing – if he returns by a sharp angle (e.g. North by east), he will return to the intended course faster than at a more gentle gradient (e.g. East by north). Whichever angle he chooses, he must deduce exactly how long he must sail on that bearing in order to reach his old course. If he sails too long, he risks overshooting it.
This is what the third column of the toleta is for. The return angles are expressed as quarters from the intended course bearing (not the current course bearing). In our example, the mariner intended to go east, but has been sailing southeast-by-east for 100 miles. Given the winds, he decides it is best to return to the original course by re-orienting the ship east-northeast (ENE, "Greco-Levante"). ENE is two quarter-winds above the intended bearing, East, so now he looks at second row ("quarters = 2") on the table. In the third column, the ritorno, shows the number 26. This represents the required number of miles he must travel on ENE bearing for every 10 miles of alargar. Remember, his alargar (distance from intended course) was 55 miles. So in order to return to his intended course he must travel 5.5 × 26 = 143 miles on ENE. In other words, he needs to hold his ENE bearing for 143 miles; once that distance is travelled, he should straighten his ship East, and he will be exactly on the intended course.
The final column (avanzo di ritorno) gives the length on the intended course he has made good by his return travel. This is also expressed in terms per 10 miles alargar. His alargar was 55, and his angle of return was ENE (thus q = 2), that means his avanzo di ritorno is 5.5 × 24 = 132. In other words, if everything goes right, and our mariner holds his ENE bearing for 143 miles (ritorno), then during that return, he will have covered an additional 132 miles on his intended eastward course (avanzo di ritorno).
Finally, the total avanzo on the eastward bearing is the avanzar during the deviation (83 miles) plus the avanzo di ritorno (132 miles), thus on the whole, he has covered 83 + 132 = 215 miles on the intended course. Measuring that distance on the map from the starting point (A), the mariner can figure out his exact current position.
This is the simplest use of the toleta de marteloio. It is, at root, a trigonometric table. However,it does not tackle the traverse problem in one go, like the Law of Sines, but rather splits the problem into two right-angled triangles which it proceeds to solve successively. Modern trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
would dispense with the step of calculating the alargar, and calculate the ritorno directly – but for that, one needs to be armed with a full sine table. The toleta is a rather simple table, easy to consult and perform calculations with, and sufficiently compact to be memorized by navigators (as Bianco recommends).
Rule of three
The toleta de marteloio is expressed for nice round numbers, 100 and 10. But, in practice, a ship would not usually sail 100 miles before trying to return, but some other distance, say 65 miles. To calculate this is a simple problem of solving ratioRatio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
s. For example, if the ship had sailed 65 miles on southeast-by-east, then calculating the alargar from the intended Eastward course is simply a matter of solving the following for :
where 26 is the alargar for 100 miles (as given in the second column of the table). This is easily done by the simple "Rule of Three", a method of cross-multiplication, using three numbers to solve for the fourth by successive multiplication and division:
So, sailing for 65 miles on SE by E implies alargar = = 16.9 miles. The avanzar, etc. can be figured out analogously.
While the "rule of three" was already known in the 14th C., skill in executing multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
and division
Division
-Mathematics:*Division , the inverse of multiplication*Division , digital implementation of mathematical division*Division, in relational algebra-Science:*Cell division, the process in which biological cells multiply...
could be elusive for Medieval sailors drawn from what was a largely illiterate society. Nonetheless, it was not inaccessible. As Andrea Bianco urged, navigators should "know how to multiply well and divide well" ("saver ben moltiplichar e ben partir") It is here where we see the important interface of commerce
Commerce
While business refers to the value-creating activities of an organization for profit, commerce means the whole system of an economy that constitutes an environment for business. The system includes legal, economic, political, social, cultural, and technological systems that are in operation in any...
and navigation. The mathematics of commerce – Arabic numerals
Arabic numerals
Arabic numerals or Hindu numerals or Hindu-Arabic numerals or Indo-Arabic numerals are the ten digits . They are descended from the Hindu-Arabic numeral system developed by Indian mathematicians, in which a sequence of digits such as "975" is read as a numeral...
, multiplication, division, fractions
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
, the tools needed to calculate purchases and sales of goods and other commercial transactions – was essentially the same as the mathematics of navigation. And this kind of mathematics was taught at the abacus school
Abacus School
Abacus or abaco refers to calculations, especially the subject of direct calculations, using Hindu numerals without the help of the abacus . Abacus school is a term applied to any Italian school or tutorial after the 13th century, whose commerce-directed curriculum placed special emphasis on...
s which were set up in the 13th C. in the commercial centers of northern Italy to train the sons of merchants, the very same class where Italian navigators were drawn from. As historian E.G.R. Taylor notes, "sailors were the first professional group to use mathematics in their everyday work"
Circle and square
For those troubled by the high art of manipulating numbers, there was an alternative. This was the visual device known as the "circle and square" (tondo e quadro), also supplied by Andrea Bianco in his 1436 atlas.The circle was a 32-wind compass rose
Compass rose
A compass rose, sometimes called a windrose, is a figure on a compass, map, nautical chart or monument used to display the orientation of the cardinal directions — North, East, South and West - and their intermediate points. It is also the term for the graduated markings found on the traditional...
(or gathering of rhumb-lines). The circle was inscribed with a 8 × 8 square grid.
The compass rose in the center can be overlooked – indeed, the circle itself can be ignored, as it is seems to have no other purpose than the construction of the rays that run across the grid. The rose of interest is in the upper left corner of the square grid. From that corner, emanate a series of compass rhumb lines. In his original 1436 tondo e quadro, Bianco has sixteen emanating rays – that is, Bianco includes half-quarter winds, or eighth-winds (otava), so that the emanating rays are at intervals of 5.625 degrees. Other constructions of the circle-and-square, e.g. the Cornaro Atlas
Cornaro Atlas
The Cornaro Atlas is an extensive Venetian collection of nautical charts and tracts, currently held by the British Library.- Background :The Cornaro Atlas is an 80-page Venetian manuscript volume, estimated to date c.1489...
, use only eight rays emanating at quarter-wind distances (11.25 degrees). Visually, these rays replicate the bottom right quarter of a 32-wind compass rose
Compass rose
A compass rose, sometimes called a windrose, is a figure on a compass, map, nautical chart or monument used to display the orientation of the cardinal directions — North, East, South and West - and their intermediate points. It is also the term for the graduated markings found on the traditional...
: East (0q), E by S (1q), ESE (2q), SE by E (3q), SE (4q), SE by S (5q), SSE (6q), S by E (7q) and South (8q).
Above the grid is a distance bar scale
Linear scale
A linear scale, also called a bar scale, scale bar, graphic scale, or graphical scale, is a means of visually showing the scale of a map, nautical chart, engineering drawing, or architectural drawing....
, notched with sub-units. There are two sets of numbers on the scale, one for measuring each grid square by 20 miles, another for measuring each grid square by 100 miles (see diagram). The top bar is the 20m-per-square scale, with every black dot denoting one mile. The bottom bar is the 100m-per-square scale, where the length of a unit square is divided into two equal 50m sub-squares, and a set of dots and red lines break it down further into lengths of 10 miles. So depending on which scale one chooses, the length of the side of the entire grid (eight squares) could be measured up to 160 miles (using the 20m-per-square scale) or up to 800 miles (using the 100m-per-square scale).
The cherub with the dividers suggests how a navigator is supposed to use the grid to calculate alargar and avanzar by visual measurement rather than manipulating numbers.
Example: suppose the ship has travelled 120 miles at two quarter-winds below the intended course (e.g. traveled at ESE, when the intended course is East). Using the dividers and the 20m scale, the navigator can measure out 120 miles with his dividers. Then setting one end at the top left corner (A), he lays out the dividers along the ESE ray (= two quarter-winds below the East ray, or horizontal top of the grid) and marks the spot (point B on the diagram). Then using a straightedge
Straightedge
A straightedge is a tool with an edge free from curves, or straight, used for transcribing straight lines, or checking the straightness of lines...
ruler draws a line up to the East ray, and marks the corresponding spot C.
It is easy to see immediately that a right-angled triangle ABC has been created. The length BC is the alargar (distance from intended course), which can be measured as 46 miles (this can be visually seen as two grid squares plus a bit, that is 20m + 20m and a little bit which can be assessed as 6m by using the dividers and the 20m bar scale). The length AC is the avanzar (distance made good), which is 111 miles – visually, five grid squares and a bit, or (20 × 5) + 11, measured by dividers and scale again.
This is how the "circle and square" dispenses manipulating numbers by multiplication and division or the rule of three. The navigator can assess the avanzar and alargar visually, by measurement alone.
This method can be used for any intended bearing and deviation, as the only purpose is to solve the triangle by dividers and scale. e.g. using our first Corsica-to-Genoa example, where intended bearing was North but the ship actually sailed Northwest, the navigator would set the dividers at length 70 miles and lay it along the fourth quarter wind (= SE ray in the tondo e quadro, as NW is four quarter winds away from North). He would calculate the alargar and avanzar in exactly the same way – draw a line to the horizontal top of the grid, measure the squares, etc.
The tondo e quadro device is very similar to the Arab sine quadrant (Rubul mujayyab), with the corner rays replicating the role of the adjustable plumb line.
Other applications
While the toleta de marteloio (and its visual counterpart, the tondo e quadro) are designed for the explicit task of recovering an intended course, they can be used in more ways, for many classes of navigational problems, e.g. plotting out a course with multiple-bearing changes, etc.Triangulation
One of the interesting applications of the rule of marteloio is for triangulationTriangulation
In trigonometry and geometry, triangulation is the process of determining the location of a point by measuring angles to it from known points at either end of a fixed baseline, rather than measuring distances to the point directly...
, e.g. determining the distance of the ship from shore landmark. (This was the final exercise attempted by Michael of Rhodes, which we replicate here with slightly different numbers.)
Example: Suppose a ship sailing NW ("Maestro") spots a landmark due West ("Ponente") one evening, but distance unknown. Suppose the ship continues sailing on the NW route overnight, and the next morning, 40 miles later, it notices that landmark is now west-southwest (WSW, "Ponente-Libeccio") of its current position. Finding the distance of the landmark from the ship is just an application of the rule of marteloio.
To solve the problem, start from the evening position (A on the map) and treat the distance between the ship and the landmark (length AB) as the intended course, and the actual route of the ship (NW) as a deviation. To figure out the distance of the landmark from the ship's position in the morning (C) is a matter of treating the distance BC as the calculated ritorno. Since we need to know the alargar to calculate the ritorno, this is a two-step procedure.
First, notice that NW is four quarter-winds above W, so looking up on the toleta, in the q = 4 row, the alargar is 71 miles for every 100 miles on the NW course. But the ship only sailed 40 miles overnight, so we have to solve the ratio 71/100 = x/40, which by the rule of three
Rule of Three
Rule of three may refer to:*Rule of three , for calculating a confidence limit when no events have been observed*Rule of Three , a tenet of Wicca*Rule of three , a computation method in mathematics...
means x = alargar = 28.4 miles. In other words, by the overnight sailing NW by 40 miles from A to C, the ship is now 28.4 miles away from its "intended" Westward course.
Now for the ritorno. The landmark, as noted, is WSW of the ship's morning position (C). So to "return" to the landmark, the ship must change its bearing from its current NW bearing to a WSW bearing – that is, 6 quarter-winds below NW. However, the toleta specifies quarter winds in terms of "intended" direction (in this case, West), and WSW is two quarter winds below West, so we need to look at the q = 2 row. This means the ritorno is 26 miles for every 10 miles alargar. Since the alargar is 28.4, that means the ritorno is 26 × 2.84 = 73.84. And there we have it. The landmark is 73.84 miles away from the ship's morning position.
(To complete the story, we might wish to find out the distance that landmark was the evening before (i.e. from point A to landmark B). That is simply a matter of adding the avanzar and the avanzo in ritorno. Quick calculations show the avanzar (@ q = 4, for 40 miles) is 28.4 miles (= 71 × 40/100) and the avanzo di ritorno (@ q = 2 for 28.4 miles alargar), is 2.84 × 24 = 68.16. So total avanzo = 28.4 + 68.16 = 96.56 miles. That was the distance between the landmark and the ship the evening before.)
Finding locations
The rule of marteloio can also be used with the avanzar as a target, e.g. suppose a ship sets out with the intention of finding the Tordesillas Line, the meridianMeridian (geography)
A meridian is an imaginary line on the Earth's surface from the North Pole to the South Pole that connects all locations along it with a given longitude. The position of a point along the meridian is given by its latitude. Each meridian is perpendicular to all circles of latitude...
legally set in a 1494 treaty at 370 leagues west of Cape Verde
Cape Verde
The Republic of Cape Verde is an island country, spanning an archipelago of 10 islands located in the central Atlantic Ocean, 570 kilometres off the coast of Western Africa...
. The ship need not set out from Cape Verde and set sail constantly at West bearing to find it. Rather, it can sail out at a more convenient bearing (e.g. SW), and treat West as an "intended" course. So using the marteloio rule, it can sail on until the avanzar on the "intended" West course reaches 370 leagues.
Indeed it need not even set out from Cape Verde, but can set out from another place, say, Seville
Seville
Seville is the artistic, historic, cultural, and financial capital of southern Spain. It is the capital of the autonomous community of Andalusia and of the province of Seville. It is situated on the plain of the River Guadalquivir, with an average elevation of above sea level...
, and use the known distance and bearing of Cape Verde (viz. Seville) and the rule of marteloio to calculate when it has finally reached the Tordesillas meridian. This takes a couple of steps. Suppose Cape Verde (B on map) is 400 leagues Southwest of Seville (A on map), but the ship intends to go straight West from Seville to reach the Tordesillas meridian in the open sea. How long does it need to sail?
The way to solve this by the rule of marteloio is to pose the problem in reverse: treat West as intended bearing and SW as the actual course. SW is four quarter-winds below W, so looking up the toleta for q = 4, the avanzar is 71 for every 100 miles sailed. So if a ship sailed 400 leagues on the "actual" SW course to Cape Verde, it would achieve an avanzar of 284 leagues (= 71 × 4) on the "intended" Westward course. Of course, the ship is not actually sailing SW to Cape Verde, but sailing W into the open sea. In other words, when the ship sets sail West from Seville, it knows it needs to sail 284 leagues on the West bearing before it reaches the implied Cape Verde meridian
Meridian (geography)
A meridian is an imaginary line on the Earth's surface from the North Pole to the South Pole that connects all locations along it with a given longitude. The position of a point along the meridian is given by its latitude. Each meridian is perpendicular to all circles of latitude...
(point C on map), and should only start counting the 370 leagues to the Tordesillas line thereafter. In other words, it needs to sail a total of 284 + 370 = 654 leagues West of Seville to reach the Tordesillas line (point D on map).
While this particular example shows the flexibility of the rule of marteloio, it also shows one of its principal drawbacks: the result completely ignores the curvature of the earth, i.e. the fact that the longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
meridian lines converge on the North Pole
North Pole
The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is, subject to the caveats explained below, defined as the point in the northern hemisphere where the Earth's axis of rotation meets its surface...
, and thus narrow at higher latitudes. Contrary to what the marteloio suggests, 370 leagues West of Cape Verde is not on the same longitude meridian as 654 leagues West of Seville. Because Seville is well north of Cape Verde, the meridians are clustered closer together at Seville's latitude than at Cape Verde's latitude. A ship sailing west of Seville will, in fact, reach the real Tordesillas meridian (point T on map) well before 654 leagues are sailed (point D).
The rule of marteloio has sailors plot routes by drawing plane triangles on a chart, as if the world's surface were flat. While this might be practical enough for sailing confined to the compact latitudes of the Mediterranean Sea
Mediterranean Sea
The Mediterranean Sea is a sea connected to the Atlantic Ocean surrounded by the Mediterranean region and almost completely enclosed by land: on the north by Anatolia and Europe, on the south by North Africa, and on the east by the Levant...
, it is quite misleading on a grander scale.
Relation to the "regiment of the leagues"
In the late 15th and 16th centuries, the improvement of nautical astronomyCelestial navigation
Celestial navigation, also known as astronavigation, is a position fixing technique that has evolved over several thousand years to help sailors cross oceans without having to rely on estimated calculations, or dead reckoning, to know their position...
and the introduction of latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
parallels allowed navigators to determine their position at sea by celestial readings, rather than relying on estimation of distance sailed. The successor of the rule of marteloio was the "Regiment of the Leagues" (regimento das léguas), that was used by Portuguese navigators sailing in the Atlantic Ocean. Or, to use the term introduced by William Bourne
William Bourne
William Bourne may refer to:*William Bourne *William Bourne *William Bourne , see Denby Pottery Company*Bill Bourne *Bill Bourne, Canadian musician and songwriter...
(1571), the "Rule to Raise or Lay a Degree", also known as the "Table of Leagues" or the "Rule for Raising the Pole". It was first written down in the Portuguese
Kingdom of Portugal
The Kingdom of Portugal was Portugal's general designation under the monarchy. The kingdom was located in the west of the Iberian Peninsula, Europe and existed from 1139 to 1910...
navigation manual Regimento do astrolabio e do quadrante (published in Lisbon c.1509, but written c.1480) It was popularized by Martín Cortés de Albacar
Martín Cortés de Albacar
Martín Cortés de Albacar was a Spanish cosmographer. In 1551 he published the standard navigitional textbook Arte de navigar Cortés was born in Bujaraloz, province of Zaragoza, Aragon...
in his 1551 Breve compendio la esfera y del arte de navegar.
The "Regiment of the Leagues" is not very different from the rule of marteloio. The Regiment of the Leagues always considers the west-east bearing as the "intended course" and measures set deviations from it. More specifically, the league table considers a fixed value of alargar – set at 1 latitude degree (or, in the measurements of the time, 17.5 (Portuguese) leagues
League (unit)
A league is a unit of length . It was long common in Europe and Latin America, but it is no longer an official unit in any nation. The league originally referred to the distance a person or a horse could walk in an hour...
, or equivalently 70 (Italian) miles
Nautical mile
The nautical mile is a unit of length that is about one minute of arc of latitude along any meridian, but is approximately one minute of arc of longitude only at the equator...
). It then gives for every different quarter wind of sailing direction (always designated as quarters away from the north-south axis, rather than away from the intended course), the relevar and the afastar. The relevar is the number of leagues on the actual course that a ship must sail in order to cover the pre-set 1 degree of latitude (17.5 leagues of alargar from the starting parallel). The afastar is merely the corresponding avanzar on the west-east bearing.
Example: Suppose a ship sets out on an East-southeast (ESE) bearing. That is six quarter-winds above South (remember: unlike the marteloio, the Regiment of the Leagues always measures quarter-winds away from the north–south meridian). Looking at any regiment of the leagues table (e.g. Martín Cortés de Albacar
Martín Cortés de Albacar
Martín Cortés de Albacar was a Spanish cosmographer. In 1551 he published the standard navigitional textbook Arte de navigar Cortés was born in Bujaraloz, province of Zaragoza, Aragon...
, 1551), for q = 6, the table gives the relevar as 45 leagues and the afastar as 42 leagues. This means that a ship sailing on the ESE bearing will have to sail 45.73 leagues to cover one degree of latitude (17.5 leagues of alargar from the east bearing, to use the marteloio language), and the corresponding afastar (avanzar in marteloio terms) will be 42.25 leagues.
If, instead, the ship had set out on a SE bearing, that is four quarter-winds above South, the corresponding values of the Regiment of the Leagues table at q = 4 are relevar = 24 and the afastar = 17 .
Notice that the SE bearing reaches the 1 degree alargar faster (i.e. smaller relevar) than that the ESE bearing, and will have less afastar (closer to the N–S meridian).
Mathematically,
- relevar = 17.5/cos θ
- afastar = 17.5 × tan θ
where θ = 11.25 × number of quarters-winds away from the north-south axis.
Despite the difference in terminology, notably the use of latitude degrees, the rule of marteloio and the Regiment of the Leagues are very similar – they are both about solving triangles on a plane chart. The advantage of the regiment over the marteloio is the introduction of latitude parallels in the table, so that the position can be checked by astronomical observation (via quadrant
Quadrant (instrument)
A quadrant is an instrument that is used to measure angles up to 90°. It was originally proposed by Ptolemy as a better kind of astrolabe. Several different variations of the instrument were later produced by medieval Muslim astronomers.-Types of quadrants:...
, astrolabe
Astrolabe
An astrolabe is an elaborate inclinometer, historically used by astronomers, navigators, and astrologers. Its many uses include locating and predicting the positions of the Sun, Moon, planets, and stars, determining local time given local latitude and longitude, surveying, triangulation, and to...
, etc.), and not have to rely wholly on sailor estimations of distance and direction.
With the regiment, geographical coordinates can also be used to guide navigation. For instance, the search for the Todesillas line (meridian 370 leagues west of Cape Verde) is much simplified by reference to a precise latitude. For instance, suppose two ships depart from Cape Verde (17° N), one on an West by North bearing (WbN, that is one quarter above West, or q = 7 from North axis), the other by a west-northwest bearing (WNW, two quarters above west, or q = 6 from the North axis). Using the Regiment of the Leagues, it is possible to calculate the precise latitudes when they will cross the Tordesillas meridian – simply divide 370 leagues west by the implied afastar at the different bearings. The WbN ship will reach the meridian when it achieves latitude 21° 21' N, while the WNW ship will reach it when it achieves latitude 29° N. So rather than counting leagues with hourglass and speed readings, the ships can just maintain bearing, and take periodic astronomical observations to assess their latitude.
Relation to "traverse sailing"
The toleta de marteloio is ancestral to the modern "traverse table" used in more modern navigation. In the modern nomenclature, the traverse is the "crooked path made by a ship when she sails in several successive directions" and resolving the traverse is "the method of finding a single course and distance which would bring a ship to the same place as two or more courses and distances.". In marteloio language, when "resolving the traverse", the known information given is the "actual course" and the "ritorno", while the unknowns are the "intended bearing" and "total avanzo".Traverse tables use three values for each of the crooked course segments – the Distance (Dist.), Difference of Latitude (D.Lat., movement along N–S axis) and the Departure (Dep., movement along E–W axis), the latter two calculated by the formulas:
- Difference of latitude = distance × cos θ
- Departure = distance × sin θ
where θ is the angular difference of the course from the N–S axis if the values of θ are less than 45°; if, however, the angle exceeds 45°, then θ is expressed as the angle of difference from the E–W axis, and the formulas are flipped, i.e. Difference of Latitude formula becomes the Departure, and the Departure formula is the Difference of Latitude). Or, even more simply, calculate θ as the angle of difference from the nearest principal wind (N, S, E, W), run the formulas and then place the larger number in the appropriate column (D.Lat. or Dep.).
For each course segment, the navigator inserts the relevant trio (Dist., D.Lat., Dep.) and can calculate the implied bearing from the beginning to the endpoint and the distance made good on that bearing. He then combines, by addition and substraction, all the differences of latitude and departure, to get the overall difference of latitude and departure, and converts that back to overall bearing and distance made good.
Manuscript sources
Ramon LlullRamon Llull
Ramon Llull was a Majorcan writer and philosopher, logician and tertiary Franciscan. He wrote the first major work of Catalan literature. Recently-surfaced manuscripts show him to have anticipated by several centuries prominent work on elections theory...
's suggestive 1295 remarks aside, the earliest known reference to marteloio is dated 1390, in the inventory of the estate of the mother of a certain Oberto Foglieto of Genoa, where an entry reads unum martelogium....item carta una pro navegando. The first clear appearance and explanation is the 1436 atlas of Venetian captain Andrea Bianco. Other early manuscripts have since been found relating the rule of marteloio, incude:
- an anonymous 15th C. Venetian codex, post-1428, once part of the collection of Doge Marco FoscariniMarco FoscariniMarco Foscarini was a Venetian statesman who served as the 117th Doge of Venice from May 31, 1762 until his death. He studied in his youth in Bologna, and was active as a diplomat, serving as ambassador to Rome and Turin; he also served as the procurator of St. Mark for a time...
, now lost. - the Liber of Venetian mariner Michael of Rhodes (c. 1434–36) (Ms. in private collection)
- the Adriatic portolano of Grazioso Benincasa of Ancona, compiled 1435–45 (Ms. at Biblioteca comunale Luciano BenincasaBiblioteca comunale Luciano BenincasaThe Biblioteca comunale Luciano Benincasa is located in Ancona, Italy, in the Palazzo Mengoni-Ferretti, at the central Piazza del Plebiscito .- History :...
in AnconaAnconaAncona is a city and a seaport in the Marche region, in central Italy, with a population of 101,909 . Ancona is the capital of the province of Ancona and of the region....
, Italy). - the Venetian portolano manuscript Alcune raxion de marineri by Pietro di Versi, c.1444 (Ms.It.IV. 170 at Biblioteca Nazionale MarcianaBiblioteca MarcianaThe Biblioteca Nazionale Marciana is a library and Renaissance building in Venice, northern Italy; it is one of the earliest surviving public manuscript depositories in the country, holding one of the greatest classical texts collections in the world. The library is named after St. Mark, the...
in VeniceVeniceVenice is a city in northern Italy which is renowned for the beauty of its setting, its architecture and its artworks. It is the capital of the Veneto region...
, Italy) - The Libro of Venetian naval trumpeter known as Zorzi Trombetta of Modone, dated c. 1444–9 (Cotton MS. Titus A.XXVI at the British LibraryBritish LibraryThe British Library is the national library of the United Kingdom, and is the world's largest library in terms of total number of items. The library is a major research library, holding over 150 million items from every country in the world, in virtually all known languages and in many formats,...
in London, UK) - Anonymous Venetian manuscript known as Arte Veneziana del Navigare, c. 1444–5 (Ms. C.M.17 at the Biblioteca del Museo Civico de Padova in PaduaPaduaPadua is a city and comune in the Veneto, northern Italy. It is the capital of the province of Padua and the economic and communications hub of the area. Padua's population is 212,500 . The city is sometimes included, with Venice and Treviso, in the Padua-Treviso-Venice Metropolitan Area, having...
, Italy). - Ragioni antique spettanti dall'arte del mare et fabriche de vasselli (Ms. NVT 19, at the National Maritime MuseumNational Maritime MuseumThe National Maritime Museum in Greenwich, England is the leading maritime museum of the United Kingdom and may be the largest museum of its kind in the world. The historic buildings forming part of the Maritime Greenwich World Heritage Site, it also incorporates the Royal Observatory, Greenwich,...
in Greenwich, UK). - Cornaro AtlasCornaro AtlasThe Cornaro Atlas is an extensive Venetian collection of nautical charts and tracts, currently held by the British Library.- Background :The Cornaro Atlas is an 80-page Venetian manuscript volume, estimated to date c.1489...
, a c.1489 copy of an earlier manuscript, (Ms.Egerton 73 at the British LibraryBritish LibraryThe British Library is the national library of the United Kingdom, and is the world's largest library in terms of total number of items. The library is a major research library, holding over 150 million items from every country in the world, in virtually all known languages and in many formats,...
in London) - 15th C. anonymous Venetian portolano (Ms. 3345* (Fosc.307) at the Österreichische Nationalbibliothek (ÖNB) in ViennaViennaVienna is the capital and largest city of the Republic of Austria and one of the nine states of Austria. Vienna is Austria's primary city, with a population of about 1.723 million , and is by far the largest city in Austria, as well as its cultural, economic, and political centre...
, Austria)
External Resources
- Altante Bianco, 1436 at Internetculturale.it; Higher resolution at Geoweb.sbn.venezia.it.
- McGee, D. et al. (2003 onwards) Michael of Rhodes: A medieval mariner and his manuscript website (accessed July 20, 2011). (originally hosted by Dibner Institute for the History of Science and Technology at M.I.T., now hosted by Museo Galileo Institute and Museum of the History of Science in Florence, Italy)