
Run-time algorithm specialisation
Encyclopedia
In computer science
, run-time algorithm specialization is a methodology for creating efficient algorithms for costly computation tasks of certain kinds. The methodology originates in the field of automated theorem proving
and, more specifically, in the Vampire theorem prover
project.
The idea is inspired by the use of partial evaluation
in optimising program translation.
Many core operations in theorem provers exhibit the following pattern.
Suppose that we need to execute some algorithm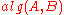 in a situation where a value of
in a situation where a value of  is fixed for potentially many different values of
is fixed for potentially many different values of  . In order to do this efficiently, we can try to find a specialization of
. In order to do this efficiently, we can try to find a specialization of 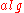 for every fixed
for every fixed  , i.e., such an algorithm
, i.e., such an algorithm 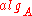 , that executing
, that executing 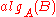 is equivalent to executing
is equivalent to executing 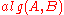 .
.
The specialized algorithm may be more efficient than the generic one, since it can exploit some particular properties of the fixed value . Typically,
. Typically, 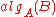 can avoid some operations that
can avoid some operations that 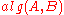 would have to perform, if they are known to be redundant for this particular parameter
would have to perform, if they are known to be redundant for this particular parameter  .
.
In particular, we can often identify some tests that are true or false for , unroll loops and recursion, etc.
, unroll loops and recursion, etc.
 on which
on which 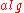 is specialised are not known statically, so the specialization takes place at run-time.
is specialised are not known statically, so the specialization takes place at run-time.
There is also an important technical difference. Partial evaluation is applied to algorithms explicitly represented as codes in some programming language. At run-time, we do not need any concrete representation of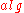 . We only have to imagine
. We only have to imagine 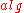 when we program the specialization procedure.
when we program the specialization procedure.
All we need is a concrete representation of the specialized version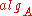 . This also means that we cannot use any universal methods for specializing algorithms, which is usually the case with partial evaluation. Instead, we have to program a specialization procedure for every particular algorithm
. This also means that we cannot use any universal methods for specializing algorithms, which is usually the case with partial evaluation. Instead, we have to program a specialization procedure for every particular algorithm 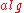 . An important advantage of doing so is that we can use some powerful ad hoc tricks exploiting peculiarities of
. An important advantage of doing so is that we can use some powerful ad hoc tricks exploiting peculiarities of 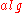 and the representation of
and the representation of  and
and  , which are beyond the reach of any universal specialization methods.
, which are beyond the reach of any universal specialization methods.
In many situations, usually when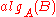 is to be computed on many values
is to be computed on many values  in a row, we can write
in a row, we can write 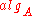 as a code of a special abstract machine
as a code of a special abstract machine
, and we often say that is compiled.
is compiled.
Then the code itself can be additionally optimized by answer-preserving transformations that rely only on the semantics of instructions of the abstract machine.
Instructions of the abstract machine can usually be represented as records. One field of such a record stores an integer tag that identifies the instruction type, other fields may be used for storing additional Parameters of the instruction, for example a pointer to another
instruction representing a label, if the semantics of the instruction requires a jump. All instructions of a code can be stored in an array, or list, or tree.
Interpretation is done by fetching instructions in some order, identifying their type
and executing the actions associated with this type.
In C
or C++ we can use a switch statement to associate
some actions with different instruction tags.
Modern compilers usually compile a switch statement with integer labels from a narrow range rather efficiently by storing the address of the statement corresponding to a value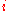 in the
in the 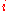 -th cell of a special array. One can exploit this
-th cell of a special array. One can exploit this
by taking values for instruction tags from a small interval of integers.
 are intended for long-term storage and the calls of
are intended for long-term storage and the calls of 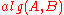 occur with different
occur with different  in an unpredictable order.
in an unpredictable order.
For example, we may have to check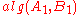 first, then
first, then 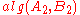 , then
, then 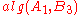 , and so on.
, and so on.
In such circumstances, full-scale specialization with compilation may not be suitable due to excessive memory usage.
However, we can sometimes find a compact specialized representation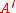
for every , that can be stored with, or instead of,
, that can be stored with, or instead of,  .
.
We also define a variant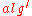 that works on this representation
that works on this representation
and any call to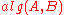 is replaced by
is replaced by 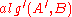 , intended to do the same job faster.
, intended to do the same job faster.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, run-time algorithm specialization is a methodology for creating efficient algorithms for costly computation tasks of certain kinds. The methodology originates in the field of automated theorem proving
Automated theorem proving
Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
and, more specifically, in the Vampire theorem prover
Vampire theorem prover
Vampire is an automatic theorem prover for first-order classical logic developed in the Computer Science Department of the University of Manchester byProf. Andrei Voronkov together with Kryštof Hoder and previously with Dr. Alexandre Riazanov...
project.
The idea is inspired by the use of partial evaluation
Partial evaluation
In computing, partial evaluation is a technique for several different types of program optimization by specialization. The most straightforward application is to produce new programs which run faster than the originals while being guaranteed to behave in the same way...
in optimising program translation.
Many core operations in theorem provers exhibit the following pattern.
Suppose that we need to execute some algorithm
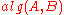 in a situation where a value of
in a situation where a value of  is fixed for potentially many different values of
is fixed for potentially many different values of  . In order to do this efficiently, we can try to find a specialization of
. In order to do this efficiently, we can try to find a specialization of 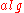 for every fixed
for every fixed  , i.e., such an algorithm
, i.e., such an algorithm 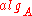 , that executing
, that executing 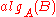 is equivalent to executing
is equivalent to executing 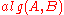 .
.The specialized algorithm may be more efficient than the generic one, since it can exploit some particular properties of the fixed value
 . Typically,
. Typically, 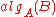 can avoid some operations that
can avoid some operations that 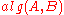 would have to perform, if they are known to be redundant for this particular parameter
would have to perform, if they are known to be redundant for this particular parameter  .
.In particular, we can often identify some tests that are true or false for
 , unroll loops and recursion, etc.
, unroll loops and recursion, etc.Difference from partial evaluation
The key difference between run-time specialization and partial evaluation is that the values of on which
on which 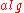 is specialised are not known statically, so the specialization takes place at run-time.
is specialised are not known statically, so the specialization takes place at run-time.There is also an important technical difference. Partial evaluation is applied to algorithms explicitly represented as codes in some programming language. At run-time, we do not need any concrete representation of
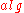 . We only have to imagine
. We only have to imagine 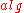 when we program the specialization procedure.
when we program the specialization procedure.All we need is a concrete representation of the specialized version
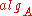 . This also means that we cannot use any universal methods for specializing algorithms, which is usually the case with partial evaluation. Instead, we have to program a specialization procedure for every particular algorithm
. This also means that we cannot use any universal methods for specializing algorithms, which is usually the case with partial evaluation. Instead, we have to program a specialization procedure for every particular algorithm 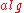 . An important advantage of doing so is that we can use some powerful ad hoc tricks exploiting peculiarities of
. An important advantage of doing so is that we can use some powerful ad hoc tricks exploiting peculiarities of 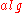 and the representation of
and the representation of  and
and  , which are beyond the reach of any universal specialization methods.
, which are beyond the reach of any universal specialization methods.Specialization with compilation
The specialized algorithm has to be represented in a form that can be interpreted.In many situations, usually when
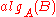 is to be computed on many values
is to be computed on many values  in a row, we can write
in a row, we can write 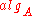 as a code of a special abstract machine
as a code of a special abstract machineAbstract machine
An abstract machine, also called an abstract computer, is a theoretical model of a computer hardware or software system used in automata theory...
, and we often say that
 is compiled.
is compiled.Then the code itself can be additionally optimized by answer-preserving transformations that rely only on the semantics of instructions of the abstract machine.
Instructions of the abstract machine can usually be represented as records. One field of such a record stores an integer tag that identifies the instruction type, other fields may be used for storing additional Parameters of the instruction, for example a pointer to another
instruction representing a label, if the semantics of the instruction requires a jump. All instructions of a code can be stored in an array, or list, or tree.
Interpretation is done by fetching instructions in some order, identifying their type
and executing the actions associated with this type.
In C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
or C++ we can use a switch statement to associate
some actions with different instruction tags.
Modern compilers usually compile a switch statement with integer labels from a narrow range rather efficiently by storing the address of the statement corresponding to a value
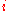 in the
in the 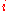 -th cell of a special array. One can exploit this
-th cell of a special array. One can exploit thisby taking values for instruction tags from a small interval of integers.
Data-and-algorithm specialization
There are situations when many instances of are intended for long-term storage and the calls of
are intended for long-term storage and the calls of 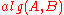 occur with different
occur with different  in an unpredictable order.
in an unpredictable order.For example, we may have to check
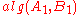 first, then
first, then 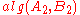 , then
, then 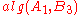 , and so on.
, and so on.In such circumstances, full-scale specialization with compilation may not be suitable due to excessive memory usage.
However, we can sometimes find a compact specialized representation
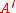
for every
 , that can be stored with, or instead of,
, that can be stored with, or instead of,  .
.We also define a variant
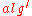 that works on this representation
that works on this representationand any call to
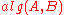 is replaced by
is replaced by 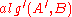 , intended to do the same job faster.
, intended to do the same job faster.See also
- PsycoPsycoPsyco is a specializing just-in-time compiler for Python originally developed by Armin Rigo and further maintained and developed by Christian Tismer....
, a specializing run-time compiler for PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive... - multi-stage programming
Further reading
- A. Riazanov and A. Voronkov, "Efficient Checking of Term Ordering Constraints", Proc. IJCAR 2004, Lecture Notes in Artificial Intelligence 3097, 2004 (compact but self-contained illustration of the method)
- A. Riazanov and A. Voronkov, Efficient Instance Retrieval with Standard and Relational Path Indexing, Information and Computation, 199(1-2), 2005 (contains another illustration of the method)
- A. Riazanov, "Implementing an Efficient Theorem Prover", PhD thesis, The University of Manchester, 2003 (contains the most comprehensive description of the method and many examples)

