
S plane
Encyclopedia
In mathematics
and engineering
, the S plane is the name for the complex plane
on which Laplace transforms are graphed. It is a mathematical domain where, instead of viewing processes in the time domain
modelled with time-based functions, they are viewed as equations in the frequency domain
. It is used as a graphical analysis tool in engineering and physics.
A real function (f) in time 't' is translated into the 's' plane by taking the integral
of the function, multiplied by from
from  to
to  , where s is a complex number
, where s is a complex number
.
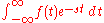
One way to understand what this equation is doing is to remember how Fourier analysis works. In Fourier analysis, harmonic sine and cosine waves are multiplied into the signal, and the resultant integration provides indication of a signal present at that frequency (i.e. the signal's energy at a point in the frequency domain). The 's' transform does the same thing, but more generally. The e-st not only catches frequencies, but also the real e-t effects as well. 's' transforms therefore cater not only for frequency response, but decay effects as well. For instance, a damped sine wave can be modeled correctly using 's' transforms.
's' transforms are commonly known as Laplace transforms. In the 's' plane, multiplying by s has the effect of differentiating in the corresponding real time domain. Dividing by s integrates.
Analysing the complex
roots of an 's' plane equation and plotting them on an Argand diagram, can reveal information about the frequency response and stability of a real time system.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, the S plane is the name for the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
on which Laplace transforms are graphed. It is a mathematical domain where, instead of viewing processes in the time domain
Time domain
Time domain is a term used to describe the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various...
modelled with time-based functions, they are viewed as equations in the frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
. It is used as a graphical analysis tool in engineering and physics.
A real function (f) in time 't' is translated into the 's' plane by taking the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of the function, multiplied by
 from
from  to
to  , where s is a complex number
, where s is a complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
.
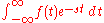
One way to understand what this equation is doing is to remember how Fourier analysis works. In Fourier analysis, harmonic sine and cosine waves are multiplied into the signal, and the resultant integration provides indication of a signal present at that frequency (i.e. the signal's energy at a point in the frequency domain). The 's' transform does the same thing, but more generally. The e-st not only catches frequencies, but also the real e-t effects as well. 's' transforms therefore cater not only for frequency response, but decay effects as well. For instance, a damped sine wave can be modeled correctly using 's' transforms.
's' transforms are commonly known as Laplace transforms. In the 's' plane, multiplying by s has the effect of differentiating in the corresponding real time domain. Dividing by s integrates.
Analysing the complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
roots of an 's' plane equation and plotting them on an Argand diagram, can reveal information about the frequency response and stability of a real time system.

