
Saint-Venant's theorem
Encyclopedia
In solid mechanics
, it is common to analyze the properties of beams
with constant cross section. Saint-Venant's theorem states that the simply connected cross section with maximal torsion
al rigidity
is a circle. It is named after the French mathematician Adhémar Jean Claude Barré de Saint-Venant
.
Given a simply connected domain D in the plane with area A , the radius and
the radius and  the area of its greatest inscribed circle, the torsional rigidity P
the area of its greatest inscribed circle, the torsional rigidity P
of D is defined by
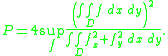
here the supremum
is taken over all the continuously differentiable functions vanishing on the boundary of D. The existence of this suppremum is a consequence of Poincaré inequality
.
Saint-Venant conjectured in 1856 that
of all domains D of equal area A the circular one has the greatest torsional rigidity, that is

A rigorous proof of this inequality was not given until 1948 by Polya. Another proof was given by Davenport
and reported in . A more general proof and an estimate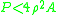
is given by Makai.
Solid mechanics
Solid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...
, it is common to analyze the properties of beams
Beam (structure)
A beam is a horizontal structural element that is capable of withstanding load primarily by resisting bending. The bending force induced into the material of the beam as a result of the external loads, own weight, span and external reactions to these loads is called a bending moment.- Overview...
with constant cross section. Saint-Venant's theorem states that the simply connected cross section with maximal torsion
Torsion (mechanics)
In solid mechanics, torsion is the twisting of an object due to an applied torque. In sections perpendicular to the torque axis, the resultant shear stress in this section is perpendicular to the radius....
al rigidity
Rigidity
Rigid or rigidity may refer to:*Stiffness, the property of a solid body to resist deformation, which is sometimes referred to as rigidity*Structural rigidity, a mathematical theory of the stiffness of ensembles of rigid objects connected by hinges...
is a circle. It is named after the French mathematician Adhémar Jean Claude Barré de Saint-Venant
Adhémar Jean Claude Barré de Saint-Venant
Adhémar Jean Claude Barré de Saint-Venant was a mechanician and mathematician who contributed to early stress analysis and also developed the one-dimensional unsteady open channel flow shallow water equations or Saint-Venant equations that are a fundamental set of equations used in modern...
.
Given a simply connected domain D in the plane with area A ,
 the radius and
the radius and  the area of its greatest inscribed circle, the torsional rigidity P
the area of its greatest inscribed circle, the torsional rigidity Pof D is defined by
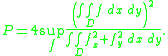
here the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
is taken over all the continuously differentiable functions vanishing on the boundary of D. The existence of this suppremum is a consequence of Poincaré inequality
Poincaré inequality
In mathematics, the Poincaré inequality is a result in the theory of Sobolev spaces, named after the French mathematician Henri Poincaré. The inequality allows one to obtain bounds on a function using bounds on its derivatives and the geometry of its domain of definition. Such bounds are of great...
.
Saint-Venant conjectured in 1856 that
of all domains D of equal area A the circular one has the greatest torsional rigidity, that is

A rigorous proof of this inequality was not given until 1948 by Polya. Another proof was given by Davenport
Harold Davenport
Harold Davenport FRS was an English mathematician, known for his extensive work in number theory.-Early life:...
and reported in . A more general proof and an estimate
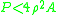
is given by Makai.

