Poincaré inequality
Encyclopedia
In mathematics
, the Poincaré inequality is a result in the theory of Sobolev space
s, named after the French
mathematician
Henri Poincaré
. The inequality allows one to obtain bounds on a function using bounds on its derivatives and the geometry of its domain of definition. Such bounds are of great importance in the modern, direct methods of the calculus of variations
. A very closely related result is the Friedrichs' inequality
.
connected open subset
of the n-dimension
al Euclidean space
Rn with a Lipschitz boundary (i.e., Ω is a Lipschitz
domain). Then there exists a constant C, depending only on Ω and p, such that for every function u in the Sobolev space W1,p(Ω),
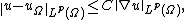
where
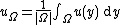
is the average value of u over Ω, with |Ω| standing for the Lebesgue measure
of the domain Ω.
of the unit torus
T2 with Fourier transform
û satisfying
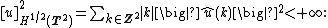
there exists a constant C such that, for every u ∈ H1/2(T2) with u identically zero on an open set E ⊆ T2,
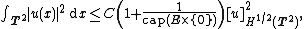
where cap(E × {0}) denotes the harmonic capacity of E × {0} when thought of as a subset of R3.
, convex
, Lipschitz domain with diameter d, then the Poincaré constant is at most d/2 for p = 1, d/π for p = 2 , and this is the best possible estimate on the Poincaré constant in terms of the diameter alone. For smooth functions, this can be understood as an application of the isoperimetric inequality to the function's level sets. http://maze5.net/?page_id=790 In one dimension, this is Wirtinger's inequality for functions.
However, in some special cases the constant C can be determined concretely. For example, for p = 2, it is well known that over the domain of unit isosceles right triangle, C = 1/π ( < d/π where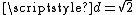
). (See, for instance,.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Poincaré inequality is a result in the theory of Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s, named after the French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
. The inequality allows one to obtain bounds on a function using bounds on its derivatives and the geometry of its domain of definition. Such bounds are of great importance in the modern, direct methods of the calculus of variations
Direct method in calculus of variations
In the calculus of variations, a topic in mathematics, the direct method is a general method for constructing a proof of the existence of a minimizer for a given functional, introduced by Zaremba and David Hilbert around 1900. The method relies on methods of functional analysis and topology...
. A very closely related result is the Friedrichs' inequality
Friedrichs' inequality
In mathematics, Friedrichs' inequality is a theorem of functional analysis, due to Kurt Friedrichs. It places a bound on the Lp norm of a function using Lp bounds on the weak derivatives of the function and the geometry of the domain, and can be used to show that certain norms on Sobolev spaces are...
.
The classical Poincaré inequality
Assume that 1 ≤ p ≤ ∞ and that Ω is a boundedBounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
connected open subset
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of the n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn with a Lipschitz boundary (i.e., Ω is a Lipschitz
Lipschitz domain
In mathematics, a Lipschitz domain is a domain in Euclidean space whose boundary is "sufficiently regular" in the sense that it can be thought of as locally being the graph of a Lipschitz continuous function...
domain). Then there exists a constant C, depending only on Ω and p, such that for every function u in the Sobolev space W1,p(Ω),
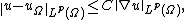
where
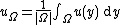
is the average value of u over Ω, with |Ω| standing for the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
of the domain Ω.
Generalizations
There exist generalizations of the Poincaré inequality to other Sobolev spaces. For example, the following (taken from ) is a Poincaré inequality for the Sobolev space H1/2(T2), i.e. the space of functions u in the L2 spaceLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
of the unit torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
T2 with Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
û satisfying
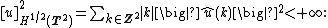
there exists a constant C such that, for every u ∈ H1/2(T2) with u identically zero on an open set E ⊆ T2,
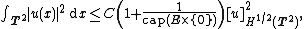
where cap(E × {0}) denotes the harmonic capacity of E × {0} when thought of as a subset of R3.
The Poincaré constant
The optimal constant C in the Poincaré inequality is sometimes known as the Poincaré constant for the domain Ω. Determining the Poincaré constant is, in general, a very hard task that depends upon the value of p and the geometry of the domain Ω. Certain special cases are tractable, however. For example, if Ω is a boundedBounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
, convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
, Lipschitz domain with diameter d, then the Poincaré constant is at most d/2 for p = 1, d/π for p = 2 , and this is the best possible estimate on the Poincaré constant in terms of the diameter alone. For smooth functions, this can be understood as an application of the isoperimetric inequality to the function's level sets. http://maze5.net/?page_id=790 In one dimension, this is Wirtinger's inequality for functions.
However, in some special cases the constant C can be determined concretely. For example, for p = 2, it is well known that over the domain of unit isosceles right triangle, C = 1/π ( < d/π where
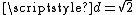). (See, for instance,.)