
Lipschitz domain
Encyclopedia
In mathematics
, a Lipschitz domain (or domain with Lipschitz boundary) is a domain in Euclidean space
whose boundary is "sufficiently regular" in the sense that it can be thought of as locally being the graph of a Lipschitz continuous function
. The term is named after the German
mathematician
Rudolf Lipschitz
.
and bounded
subset
of Rn. Let ∂Ω denote the boundary
of Ω. Then Ω is said to have Lipschitz boundary, and is called a Lipschitz domain, if, for every point p ∈ ∂Ω, there exists a radius r > 0 and a map hp : Br(p) → Q such that
where

denotes the n-dimension
al open ball of radius r about p, Q denotes the unit ball B1(0), and
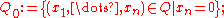
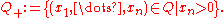
require that the domain of study be a Lipschitz domain. Consequently, many partial differential equation
s and variational problems
are defined on Lipschitz domains.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Lipschitz domain (or domain with Lipschitz boundary) is a domain in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
whose boundary is "sufficiently regular" in the sense that it can be thought of as locally being the graph of a Lipschitz continuous function
Lipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
. The term is named after the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Rudolf Lipschitz
Rudolf Lipschitz
Rudolf Otto Sigismund Lipschitz was a German mathematician and professor at the University of Bonn from 1864. Peter Gustav Dirichlet was his teacher. He supervised the early work of Felix Klein....
.
Definition
Let n ∈ N, and let Ω be an openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
and bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of Rn. Let ∂Ω denote the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of Ω. Then Ω is said to have Lipschitz boundary, and is called a Lipschitz domain, if, for every point p ∈ ∂Ω, there exists a radius r > 0 and a map hp : Br(p) → Q such that
- hp is a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
; - hp and hp−1 are both Lipschitz continuous functions;
- hp(∂Ω ∩ Br(p)) = Q0;
- hp(Ω ∩ Br(p)) = Q+;
where

denotes the n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al open ball of radius r about p, Q denotes the unit ball B1(0), and
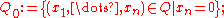
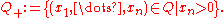
Applications of Lipschitz domains
Many of the Sobolev embedding theoremsSobolev inequality
In mathematics, there is in mathematical analysis a class of Sobolev inequalities, relating norms including those of Sobolev spaces. These are used to prove the Sobolev embedding theorem, giving inclusions between certain Sobolev spaces, and the Rellich–Kondrachov theorem showing that under...
require that the domain of study be a Lipschitz domain. Consequently, many partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s and variational problems
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
are defined on Lipschitz domains.

