
Satake isomorphism
Encyclopedia
In mathematics, the Satake isomorphism, introduced by , identifies the Hecke algebra
of a reductive group
over a local field
with a ring of invariants of the Weyl group
.
The geometric Satake equivalence is a geometric version of the Satake isomorphism, introduced by .
, K be a non-Archimedian local field and O its ring of integers. Then the Satake isomorphism identifies the Grothendieck group of complex representations of the Langlands dual of G, with the ring of G(O) invariant compactly supported functions on the affine Grassmanian. In formulas:
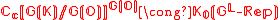
Here G(O) acts on G(K) / G(O) by multiplication from the left.
Hecke algebra of a locally compact group
In mathematics, a Hecke algebra of a locally compact group is an algebra of binvariant measures under convolution.Let be a pair consisting of a unimodular locally compact topological group G and a closed subgroup K of G...
of a reductive group
Reductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
over a local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
with a ring of invariants of the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
.
The geometric Satake equivalence is a geometric version of the Satake isomorphism, introduced by .
Statement
Let G be a Chevallier groupGroup of Lie type
In mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
, K be a non-Archimedian local field and O its ring of integers. Then the Satake isomorphism identifies the Grothendieck group of complex representations of the Langlands dual of G, with the ring of G(O) invariant compactly supported functions on the affine Grassmanian. In formulas:
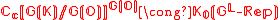
Here G(O) acts on G(K) / G(O) by multiplication from the left.

