Scalar field solution
Encyclopedia
In general relativity
, a scalar field solution is an exact solution
of the Einstein field equation in which the gravitational field is due entirely to the field energy and momentum of a scalar field
. Such a field may or may not be massless, and it may be taken to have minimal curvature coupling, or some other choice, such as conformal coupling.
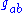(or by defining a frame field
). The curvature tensor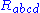
of this manifold and associated quantities such as the Einstein tensor
, are well-defined even in the absence of any physical theory, but in general relativity they acquire a physical interpretation as geometric manifestations of the gravitational field
.
In addition, we must specify a scalar field by giving a function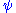
. This function is required to satisfy two following conditions:
.
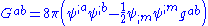Both conditions follow from varying the Lagrangian density for the scalar field, which in the case of a minimally coupled massless scalar field is
Here,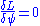
gives the wave equation, while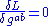
gives the Einstein equation (in the case where the field energy of the scalar field is the only source of the gravitational field).
, to some quantum field. In general relativity, the speculative quintessence
field can appear as a scalar field. For example, a flux of neutral pion
s can in principle be modeled as a minimally coupled massless scalar field.
rather than the coordinate basis are often called physical components, because these are the components which can (in principle) be measured by an observer.
In the special case of a minimally coupled massless scalar field, an adapted frame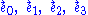
(the first is a timelike unit vector field
, the last three are spacelike unit vector fields)
can always be found in which the Einstein tensor takes the simple form
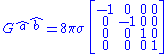
where
is the energy density of the scalar field.
of the Einstein tensor in a minimally coupled massless scalar field solution must have the form
In other words, we have a simple eigvalue and a triple eigenvalue, each being the negative of the other. Multiply out and using Gröbner basis
methods, we find that the following three invariants must vanish identically:
Using Newton's identities
, we can rewrite these in terms of the traces of the powers. We find that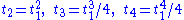
We can rewrite this in terms of index gymanastics as the manifestly invariant criteria:
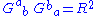
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, a scalar field solution is an exact solution
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
of the Einstein field equation in which the gravitational field is due entirely to the field energy and momentum of a scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
. Such a field may or may not be massless, and it may be taken to have minimal curvature coupling, or some other choice, such as conformal coupling.
Mathematical definition
In general relativity, the geometric setting for physical phenomena is a Lorentzian manifold, which is physically interpreted as a curved spacetime, and which is mathematically specified by defining a metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
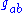(or by defining a frame fieldFrame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
). The curvature tensor
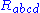
of this manifold and associated quantities such as the Einstein tensor
Einstein tensor
In differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
, are well-defined even in the absence of any physical theory, but in general relativity they acquire a physical interpretation as geometric manifestations of the gravitational fieldGravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
.
In addition, we must specify a scalar field by giving a function
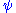. This function is required to satisfy two following conditions:
- The function must satisfy the (curved spacetime) source-free wave equationWave equationThe wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, - The Einstein tensor must match the stress-energy tensor for the scalar field, which in the simplest case, a minimally coupled massless scalar field, can be written
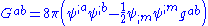.Both conditions follow from varying the Lagrangian density for the scalar field, which in the case of a minimally coupled massless scalar field is
Here,
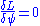
gives the wave equation, while
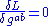
gives the Einstein equation (in the case where the field energy of the scalar field is the only source of the gravitational field).
Physical interpretation
Scalar fields are often interpreted as classical approximations, in the sense of effective field theoryEffective field theory
In physics, an effective field theory is, as any effective theory, an approximate theory, that includes appropriate degrees of freedom to describe physical phenomena occurring at a chosen length scale, while ignoring substructure and degrees of freedom at shorter distances .-The renormalization...
, to some quantum field. In general relativity, the speculative quintessence
Quintessence (physics)
In physics, quintessence is a hypothetical form of dark energy postulated as an explanation of observations of an accelerating universe. It has been proposed by some physicists to be a fifth fundamental force...
field can appear as a scalar field. For example, a flux of neutral pion
Pion
In particle physics, a pion is any of three subatomic particles: , , and . Pions are the lightest mesons and they play an important role in explaining the low-energy properties of the strong nuclear force....
s can in principle be modeled as a minimally coupled massless scalar field.
Einstein tensor
The components of a tensor computed with respect to a frame fieldFrame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
rather than the coordinate basis are often called physical components, because these are the components which can (in principle) be measured by an observer.
In the special case of a minimally coupled massless scalar field, an adapted frame
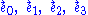
(the first is a timelike unit vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
, the last three are spacelike unit vector fields)
can always be found in which the Einstein tensor takes the simple form
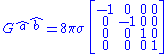
where
is the energy density of the scalar field.Eigenvalues
The characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Einstein tensor in a minimally coupled massless scalar field solution must have the form
In other words, we have a simple eigvalue and a triple eigenvalue, each being the negative of the other. Multiply out and using Gröbner basis
Gröbner basis
In computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
methods, we find that the following three invariants must vanish identically:
Using Newton's identities
Newton's identities
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials...
, we can rewrite these in terms of the traces of the powers. We find that
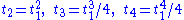
We can rewrite this in terms of index gymanastics as the manifestly invariant criteria:
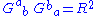
Examples
Notable individual scalar field solutions include- the Janis–Newman–Winicour scalar field solution, which is the unique static and spherically symmetric massless minimally coupled scalar field solution.