
Scale property
Encyclopedia
In the mathematical discipline of descriptive set theory
, a scale is a certain kind of object defined on a set of points in some Polish space
(for example, a scale might be defined on a set of real number
s). Scales were originally isolated as a concept in the theory of uniformization , but have found wide applicability in descriptive set theory, with applications such as establishing bounds on the possible lengths of wellorderings of a given complexity, and showing (under certain assumptions) that there are largest countable set
s of certain complexities.
for a relation
of a given complexity. That is, given a relation R, and supposing that for every x there is some y such that xRy, we would like an actual definable function f such that f(x) picks out a particular value y for which xRy.
If a relation — say, between points in the Baire space
(which for purposes of descriptive set theory is more or less equivalent to the real numbers) — is "sufficiently definable", then it will have a so-called Suslin representation, a representation in terms of trees. A Suslin representation for a relation R in turn allows giving a definable uniformization for R (with the tree as a parameter to the definition); given x, it suffices to follow the leftmost branch of the tree of attempts to find a y such that xRy.
Scales are closely related to Suslin representations. In fact, if a subset of the Baire space has a κ-scale (that is, a scale all of whose norms take values less than κ; see the formal definition below), then it also has a κ-Suslin representation (that is, it can be represented by the infinite branches through a tree on κ×ω). Conversely, if a set has a κ-Suslin representation, then it has a κω-scale.
The advantage of scales over unadorned Suslin representations is that arguments involving determinacy
can use scales on simpler pointsets to obtain scales on more complicated ones, via arguments initiated by Yiannis N. Moschovakis
.

where each Xk is either the Baire space
or a countably infinite discrete set, we say that a norm on A is a map from A into the ordinal number
s. Each norm has an associated prewellordering
, where one element of A precedes another element if the norm of the first is less than the norm of the second.
A scale on A is a countably infinite collection of norms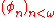
with the following properties:
By itself, at least granted the axiom of choice, the existence of a scale on a pointset is trivial, as A can be wellordered and each φn can simply enumerate A. To make the concept useful, a definability criterion must be imposed on the norms (individually and together). Here "definability" is understood in the usual sense of descriptive set theory; it need not be definability in an absolute sense, but rather indicates membership in some pointclass
of sets of reals. The norms φn themselves are not sets of reals, but the corresponding prewellordering
s are (at least in essence).
The idea is that, for a given pointclass Γ, we want the prewellorderings below a given point in A to be uniformly represented both as a set in Γ and as one in the dual pointclass of Γ, relative to the "larger" point being an element of A. Formally, we say that the φn form a Γ-scale on A if they form a scale on A and there are ternary relations S and T such that, if y is an element of A, then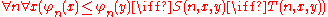
where S is in Γ and T is in the dual pointclass of Γ (that is, the complement of T is in Γ). Note here that we think of φn(x) as being ∞ whenever x∉A; thus the condition φn(x)≤φn(y), for y∈A, also implies x∈A.
Note also that the definition does not imply that the collection of norms is in the intersection of Γ with the dual pointclass of Γ. This is because the three-way equivalence is conditional on y being an element of A. For y not in A, it might be the case that one or both of S(n,x,y) or T(n,x,y) fail to hold, even if x is in A (and therefore automatically φn(x)≤φn(y)=∞).
in the given pointclass have a uniformization
that is also in the pointclass.
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
, a scale is a certain kind of object defined on a set of points in some Polish space
Polish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
(for example, a scale might be defined on a set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s). Scales were originally isolated as a concept in the theory of uniformization , but have found wide applicability in descriptive set theory, with applications such as establishing bounds on the possible lengths of wellorderings of a given complexity, and showing (under certain assumptions) that there are largest countable set
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
s of certain complexities.
Motivation
Scales arose from the question of finding a definable uniformizationUniformization (set theory)
In set theory, the axiom of uniformization, a weak form of the axiom of choice, states that if R is a subset of X\times Y, where X and Y are Polish spaces,...
for a relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
of a given complexity. That is, given a relation R, and supposing that for every x there is some y such that xRy, we would like an actual definable function f such that f(x) picks out a particular value y for which xRy.
If a relation — say, between points in the Baire space
Baire space (set theory)
In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...
(which for purposes of descriptive set theory is more or less equivalent to the real numbers) — is "sufficiently definable", then it will have a so-called Suslin representation, a representation in terms of trees. A Suslin representation for a relation R in turn allows giving a definable uniformization for R (with the tree as a parameter to the definition); given x, it suffices to follow the leftmost branch of the tree of attempts to find a y such that xRy.
Scales are closely related to Suslin representations. In fact, if a subset of the Baire space has a κ-scale (that is, a scale all of whose norms take values less than κ; see the formal definition below), then it also has a κ-Suslin representation (that is, it can be represented by the infinite branches through a tree on κ×ω). Conversely, if a set has a κ-Suslin representation, then it has a κω-scale.
The advantage of scales over unadorned Suslin representations is that arguments involving determinacy
Determinacy
In set theory, a branch of mathematics, determinacy is the study of under what circumstances one or the other player of a game must have a winning strategy, and the consequences of the existence of such strategies.-Games:...
can use scales on simpler pointsets to obtain scales on more complicated ones, via arguments initiated by Yiannis N. Moschovakis
Yiannis N. Moschovakis
Yiannis Nicholas Moschovakis is a set theorist, descriptive set theorist, and recursion theorist, at UCLA. For many years he has split his time between UCLA and University of Athens . His book Descriptive Set Theory is the primary reference for the subject...
.
Formal definition
Given a pointset A contained in some product space
where each Xk is either the Baire space
Baire space (set theory)
In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...
or a countably infinite discrete set, we say that a norm on A is a map from A into the ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s. Each norm has an associated prewellordering
Prewellordering
In set theory, a prewellordering is a binary relation that is transitive, wellfounded, and total. In other words, if \leq is a prewellordering on a set X, and if we define \sim byx\sim y\iff x\leq y \land y\leq x...
, where one element of A precedes another element if the norm of the first is less than the norm of the second.
A scale on A is a countably infinite collection of norms
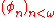
with the following properties:
- If the sequence xi is such that
- xi is an element of A for each natural number i, and
- xi converges to an element xin the product space X, and
- for each natural number n there is an ordinal λn such that φn(xi)=λn for all sufficiently large i, then
- x is an element of A, and
- for each n, φn(x)≤λn.
By itself, at least granted the axiom of choice, the existence of a scale on a pointset is trivial, as A can be wellordered and each φn can simply enumerate A. To make the concept useful, a definability criterion must be imposed on the norms (individually and together). Here "definability" is understood in the usual sense of descriptive set theory; it need not be definability in an absolute sense, but rather indicates membership in some pointclass
Pointclass
In the mathematical field of descriptive set theory, a pointclass is a collection of sets of points, where a point is ordinarily understood to be an element of some perfect Polish space. In practice, a pointclass is usually characterized by some sort of definability property; for example, the...
of sets of reals. The norms φn themselves are not sets of reals, but the corresponding prewellordering
Prewellordering
In set theory, a prewellordering is a binary relation that is transitive, wellfounded, and total. In other words, if \leq is a prewellordering on a set X, and if we define \sim byx\sim y\iff x\leq y \land y\leq x...
s are (at least in essence).
The idea is that, for a given pointclass Γ, we want the prewellorderings below a given point in A to be uniformly represented both as a set in Γ and as one in the dual pointclass of Γ, relative to the "larger" point being an element of A. Formally, we say that the φn form a Γ-scale on A if they form a scale on A and there are ternary relations S and T such that, if y is an element of A, then
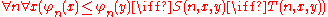
where S is in Γ and T is in the dual pointclass of Γ (that is, the complement of T is in Γ). Note here that we think of φn(x) as being ∞ whenever x∉A; thus the condition φn(x)≤φn(y), for y∈A, also implies x∈A.
Note also that the definition does not imply that the collection of norms is in the intersection of Γ with the dual pointclass of Γ. This is because the three-way equivalence is conditional on y being an element of A. For y not in A, it might be the case that one or both of S(n,x,y) or T(n,x,y) fail to hold, even if x is in A (and therefore automatically φn(x)≤φn(y)=∞).
Scale property
The scale property is a strengthening of the prewellordering property. For pointclasses of a certain form, it implies that relationsRelation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
in the given pointclass have a uniformization
Uniformization (set theory)
In set theory, the axiom of uniformization, a weak form of the axiom of choice, states that if R is a subset of X\times Y, where X and Y are Polish spaces,...
that is also in the pointclass.

