Schatten class operator
Encyclopedia
In mathematics
, specifically functional analysis
, a pth Schatten-class operator is a bounded linear operator on a Hilbert space
with finite pth Schatten norm
. The space of pth Schatten-class operators is a Banach space
with respect to the Schatten norm.
Via polar decomposition, one can prove that the space of pth Schatten class operators is an ideal in B(H). Furthermore, the Schatten norm
satisfies a type of Hölder inequality:
If we denote by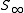
the Banach space of compact operator
s on H with respect to the operator norm
, the above Hölder-type inequality even holds for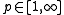
. From this it follows that 
, 
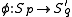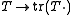is a well-defined contraction. (Here the prime denotes (topological) dual.)
Observe that the 2nd Schatten class is in fact the Hilbert space of Hilbert–Schmidt operators. Moreover, the 1st Schatten class is the space of trace class
operators.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a pth Schatten-class operator is a bounded linear operator on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
with finite pth Schatten norm
Schatten norm
In mathematics, specifically functional analysis, the Schatten norm arises as a generalization of p-integrability similar to the trace class norm and the Hilbert–Schmidt norm.-Definition:...
. The space of pth Schatten-class operators is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
with respect to the Schatten norm.
Via polar decomposition, one can prove that the space of pth Schatten class operators is an ideal in B(H). Furthermore, the Schatten norm
Schatten norm
In mathematics, specifically functional analysis, the Schatten norm arises as a generalization of p-integrability similar to the trace class norm and the Hilbert–Schmidt norm.-Definition:...
satisfies a type of Hölder inequality:
If we denote by
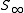the Banach space of compact operatorCompact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
s on H with respect to the operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
, the above Hölder-type inequality even holds for
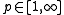. From this it follows that 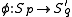, 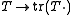is a well-defined contraction. (Here the prime denotes (topological) dual.)Observe that the 2nd Schatten class is in fact the Hilbert space of Hilbert–Schmidt operators. Moreover, the 1st Schatten class is the space of trace class
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
operators.