Schauder fixed point theorem
Encyclopedia
The Schauder fixed point theorem is an extension of the Brouwer fixed point theorem
to topological vector space
s, which may be of infinite dimension. It asserts that if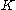
is a convex
subset of a topological vector space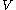
and 
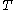is a continuous mapping of 
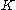into itself so that 
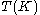is contained in a compact subset of 
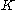, then 
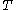has a fixed point
.
A consequence, called Schaefer's fixed point theorem, is particularly useful for proving existence of solutions to nonlinear partial differential equations.
Schaefer's theorem is in fact a special case of the far reaching Leray–Schauder theorem which was discovered earlier by Juliusz Schauder
and Jean Leray
.
The statement is as follows. Let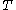
be a continuous and compact mapping of a Banach space 
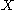into itself, such that the set
Brouwer fixed point theorem
Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
to topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s, which may be of infinite dimension. It asserts that if
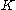is a convexConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
subset of a topological vector space
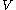and 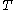is a continuous mapping of 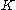into itself so that 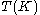is contained in a compact subset of 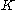, then 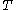has a fixed pointFixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
.
A consequence, called Schaefer's fixed point theorem, is particularly useful for proving existence of solutions to nonlinear partial differential equations.
Schaefer's theorem is in fact a special case of the far reaching Leray–Schauder theorem which was discovered earlier by Juliusz Schauder
Juliusz Schauder
Juliusz Paweł Schauder was a Polish mathematician of Jewish origin, known for his work in functional analysis, partial differential equation and mathematical physics.Born on September 21, 1899 in Lemberg, he had to fight in World War I right after his graduation from school...
and Jean Leray
Jean Leray
Jean Leray was a French mathematician, who worked on both partial differential equations and algebraic topology....
.
The statement is as follows. Let
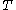be a continuous and compact mapping of a Banach space 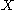into itself, such that the set-
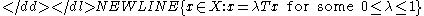
is bounded. Then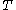
has a fixed point.
History
The theorem was conjectured and proven for special cases, such as Banach spaces, by Juliusz Schauder in 1930. His conjecture for the general case was published in the Scottish bookScottish CaféThe Scottish Café was the café in Lwów where, in the 1930s and 1940s, mathematicians from the Lwów School collaboratively discussed research problems, particularly in functional analysis and topology....
. In 1934, TychonoffAndrey Nikolayevich TychonoffAndrey Nikolayevich Tikhonov was a Soviet and Russian mathematician known for important contributions to topology, functional analysis, mathematical physics, and ill-posed problems. He was also inventor of magnetotellurics method in geology. Tikhonov originally published in German, whence the...
proved the theorem for the case when K is a compact convex subset of a locally convexLocally convex topological vector spaceIn functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
space. This version is known as the Schauder–Tychonoff fixed point theorem. B. V. Singbal proved the theorem for the more general case where K may be non-compact; the proof can be found in the appendix of Bonsall's book (see references). The full result (without the assumption of local convexity) was finally proven by Robert Cauty in 2001.