
Schiffler point
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Schiffler point of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
is a point defined from the triangle that is invariant under Euclidean transformations of the triangle. This point was first defined and investigated by Schiffler et al. (1985).
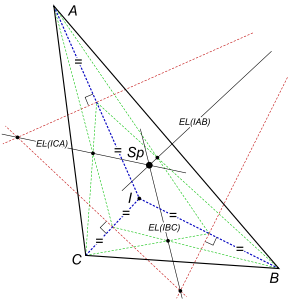
A triangle ABC with the incenter I has its Schiffler point at the point of concurrence of the Euler lines of the four triangles BCI, CAI, ABI, and ABC.
Trilinear coordinates for the Schiffler point are

or, equivalently,

where a, b, and c denote the side lengths of triangle ABC.

