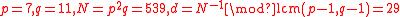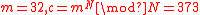The Schmidt–Samoa cryptosystem is an asymmetric cryptographic technique, whose security, like Rabin

Rabin cryptosystem

The Rabin cryptosystem is an asymmetric cryptographic technique, whose security, like that of RSA, is related to the difficulty of factorization. However the Rabin cryptosystem has the advantage that the problem on which it relies has been proved to be as hard as integer factorization, which is...

 depends on the difficulty of integer factorization

Factorization

In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...

. Unlike Rabin this algorithm does not produce an ambiguity in the decryption at a cost of encryption speed.

Key generation

• Choose two large distinct primes p and q and compute
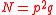
• Compute

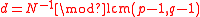
Now N is the public key and d is the private key.

Decryption

To decrypt a ciphertext c we compute the plaintext as which like for Rabin and RSA can be computed with the Chinese remainder theorem

Chinese remainder theorem

The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...

.

Example:

• 
• 

Now to verify:

• 

Security

The algorithm, like Rabin, is based on the difficulty of factoring the modulus N, which is a distinct advantage over RSA.
That is, it can be shown that if there exists an algorithm that can decrypt arbitrary messages, then this algorithm can be used to factor N.

Efficiency

The algorithm processes decryption as fast as Rabin and RSA, however it has much slower encryption since the sender must compute a full exponentiation.

Since encryption uses a fixed known exponent an addition chain

Addition-chain exponentiation

In mathematics and computer science, optimal addition-chain exponentiation is a method of exponentiation by positive integer powers that requires a minimal number of multiplications. It works by creating a shortest addition chain that generates the desired exponent. Each exponentiation in the chain...

may be used to optimize the encryption process. The cost of producing an optimal addition chain can be amortized over the life of the public key, that is, it need only be computed once and cached.