
Schur–Zassenhaus theorem
Encyclopedia
The Schur–Zassenhaus theorem is a theorem
in group theory
which states that if is a finite group
is a finite group
, and is a normal subgroup
is a normal subgroup
whose order
is coprime
to the order of the quotient group
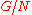 , then
, then  is a semidirect product
is a semidirect product
of and
and 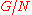 .
.
An alternative statement of the theorem is that any normal Hall subgroup
of a finite group has a complement in
has a complement in  .
.
It is clear that if we do not impose the coprime condition, the theorem is not true
: consider for example the cyclic group
 and its normal subgroup
and its normal subgroup  . Then if
. Then if  were a semidirect product of
were a semidirect product of 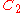 and
and 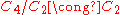 then
then  would have to contain two elements of order 2, but it only contains one.
would have to contain two elements of order 2, but it only contains one.
The Schur–Zassenhaus theorem at least partially answers the question: "In a composition series
, how can we classify groups with a certain set of composition factors?" The other part, which is where the composition factors do not have coprime orders, is tackled in extension theory.
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
which states that if
 is a finite group
is a finite groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, and
 is a normal subgroup
is a normal subgroupNormal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
whose order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
is coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to the order of the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
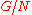 , then
, then  is a semidirect product
is a semidirect productSemidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of
 and
and 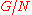 .
.An alternative statement of the theorem is that any normal Hall subgroup
Hall subgroup
In mathematics, a Hall subgroup of a finite group G is a subgroup whose order is coprime to its index. They are named after the group theorist Philip Hall.- Definitions :A Hall divisor of an integer n is a divisor d of n such that...
of a finite group
 has a complement in
has a complement in  .
.It is clear that if we do not impose the coprime condition, the theorem is not true
Truth
Truth has a variety of meanings, such as the state of being in accord with fact or reality. It can also mean having fidelity to an original or to a standard or ideal. In a common usage, it also means constancy or sincerity in action or character...
: consider for example the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
 and its normal subgroup
and its normal subgroup  . Then if
. Then if  were a semidirect product of
were a semidirect product of 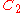 and
and 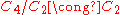 then
then  would have to contain two elements of order 2, but it only contains one.
would have to contain two elements of order 2, but it only contains one.The Schur–Zassenhaus theorem at least partially answers the question: "In a composition series
Composition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
, how can we classify groups with a certain set of composition factors?" The other part, which is where the composition factors do not have coprime orders, is tackled in extension theory.

