
Schwinger parametrization
Encyclopedia
Schwinger parametrization is a technique for evaluating loop integral
s which arise from Feynman diagram
s with one or more loops.
Using the well-known observation that
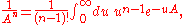
Julian Schwinger
noticed that one may simplify the integral:
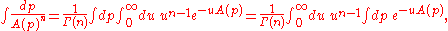
for Re(n)>0.
Another version of Schwinger parametrization is:

and it is easy to generalize this identity to n denominators.
See also Feynman parametrization
.
Loop integral
In quantum field theory and statistical mechanics, loop integrals are the integrals which appear when evaluating the Feynman diagrams with one or more loops by integrating over the internal momenta....
s which arise from Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s with one or more loops.
Using the well-known observation that
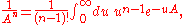
Julian Schwinger
Julian Schwinger
Julian Seymour Schwinger was an American theoretical physicist. He is best known for his work on the theory of quantum electrodynamics, in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order.Schwinger is recognized as one of the...
noticed that one may simplify the integral:
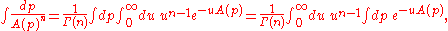
for Re(n)>0.
Another version of Schwinger parametrization is:

and it is easy to generalize this identity to n denominators.
See also Feynman parametrization
Feynman parametrization
Feynman parametrization is a technique for evaluating loop integrals which arise from Feynman diagrams with one or more loops. However, it is sometimes useful in integration in areas of pure mathematics as well.Richard Feynman observed that:...
.

