Science of Value
Encyclopedia
The science of value, or value science, is a creation of philosopher Robert S. Hartman
, which attempts to formally elucidate value theory
using both formal
and symbolic logic.
, and can be stated in symbolic logic, is that a thing is good insofar as it exemplifies its concept. This means, according to Hartman, that the good thing has a name, that the name has a meaning defined by a set of properties, and that the thing possesses all of the properties in the set. A thing is bad if it does not fulfill its definition. A car, by definition, has brakes. A car which accelerates when the brakes are applied is a bad car, since a car by definition must have brakes. A horse, if we called it a car, would be an even worse car, with fewer of the properties of a car.
He introduces three basic dimensions of value, systemic, extrinsic and intrinsic, each with their own cardinality for sets of properties; finite,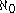
and 
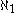. In practice, the terms "good" and "bad" apply to finite sets of properties, since this is the only case where there is a ratio between the total number of desired properties and the number of such properties possessed by some object being valued. (In the case where the number of properties is countably infinite, the extrinsic dimension of value, the exposition as well as the mere definition of a specific concept is taken into consideration. Perfection is to Systemic Value what Goodness is to Extrinsic Value and what Uniqueness is to Intrinsic Value.}
Hartman quantifies this notion by the principle that each property of the thing is worth as much as each other property, depending on the level of abstraction. Hence, if a thing has n properties, each of them—if on the same level of abstraction—is proportionally worth n-1. In other words, a car having brakes or having a gas cap are weighted equally so far as their value goes, so long as both are a part of one's definition of one's personal concept of a "car." Since a gas cap is not normally a part of a car's definition, it would be given no weight. Headlights could be weighed twice, once or not at all depending on how headlights appear in the description of a car. Given a finite set of n properties, a thing is good if it is perceived to have all of the properties, fair if it has more than n/2 of them, average if n/2 of them, and bad if it has fewer than n/2.
elements. This is the cardinality, in Hartman's system, of intrinsic value.
Further combinations are possible, leading to larger uncountable infinities; and Hartman also introduces the reciprocals of aleph number
s, which play no role in ordinary mathematics, but which Hartman employs as a sort of infinitesimal proportion, and which he contends goes to zero in the limit as the uncountable cardinals become larger. In Hartman's calculus, a Dear John letter
("we will always be friends") has axiological value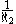
, whereas other disvalues such as commercializing the birth of the inspired founder of a religion (e.g., Christ
); or making the mistake of taking a metaphor literally; would do slightly better, with a value of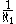
.
fallacy when they dispute him on that. A standard argument against enumeration is that new properties can be defined in terms of old ones. Philosophers speak of the problem of organic value as a result of the observation that the value of a whole does not seem to be a mere sum of the value of its parts—which again is something Hartman never claimed. Adding more features, even if each seems to be a good one, can sometimes lead to the overall value going down. In this way we get over-engineered software or the kind of DVD remote control which has too many buttons on it. Hartman holds that "the name (that one puts on a concept) sets the norm" so he would rejoin that a "Remote with too many buttons" is a disvalue.
From a mathematician's point of view, much of Hartman's work in The Structure of Value is rather novel and does not use conventional mathematical methodology, nor axiomatic reasoning, however he later employed the mathematics of topological Hausdorff sets, interpreting them as a model for the value-structure of metaphors, in a paper on Aesthetics.
Hartman, following Georg Cantor, uses infinite cardinalities. He posits—as stipulated definitions—the reciprocals of transfinite cardinal numbers. These, together with the algebraic Laws of Exponents, enables him to construct what is today known as The Calculus of Values. He does not in the STRUCTURE book clearly explain how he calculates the value of such items as Christmas shopping in terms of this calculus, although he does explain it in his paper "The Measurement of Value." While inverses of infinite quantities (infinitesimals) exist in certain systems of numbers, such as hyperreal numbers and surreal numbers, these are not reciprocals of cardinal numbers.
Hartman supporters counter that it is not necessary for properties to be actually enumerated, only that they exist and can correspond bijectively (one-to-one). The attributes in the meaning of a concept only "consist" as stipulations; they don't exist. Questions regarding the actual existence of an exemplar of a concept belong to ontology.
Intensional attributes can resemble, but are not identical to, the properties perceived by the five senses. Attributes are names of properties. When, even partially, the properties of a thing match the attributes of that thing in the mind of the one making the judgment, the thing will be said to have "value". When they completely correspond, the thing will be called "good". These are basic ideas in value science.
Robert S. Hartman
Robert Schirokauer Hartman was a logician and philosopher. His primary field of study was scientific axiology and he is known as its original theorist...
, which attempts to formally elucidate value theory
Value theory
Value theory encompasses a range of approaches to understanding how, why and to what degree people should value things; whether the thing is a person, idea, object, or anything else. This investigation began in ancient philosophy, where it is called axiology or ethics. Early philosophical...
using both formal
Formal logic
Classical or traditional system of determining the validity or invalidity of a conclusion deduced from two or more statements...
and symbolic logic.
Fundamentals
The fundamental principle, which functions as an axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
, and can be stated in symbolic logic, is that a thing is good insofar as it exemplifies its concept. This means, according to Hartman, that the good thing has a name, that the name has a meaning defined by a set of properties, and that the thing possesses all of the properties in the set. A thing is bad if it does not fulfill its definition. A car, by definition, has brakes. A car which accelerates when the brakes are applied is a bad car, since a car by definition must have brakes. A horse, if we called it a car, would be an even worse car, with fewer of the properties of a car.
He introduces three basic dimensions of value, systemic, extrinsic and intrinsic, each with their own cardinality for sets of properties; finite,
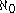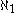and . In practice, the terms "good" and "bad" apply to finite sets of properties, since this is the only case where there is a ratio between the total number of desired properties and the number of such properties possessed by some object being valued. (In the case where the number of properties is countably infinite, the extrinsic dimension of value, the exposition as well as the mere definition of a specific concept is taken into consideration. Perfection is to Systemic Value what Goodness is to Extrinsic Value and what Uniqueness is to Intrinsic Value.}Hartman quantifies this notion by the principle that each property of the thing is worth as much as each other property, depending on the level of abstraction. Hence, if a thing has n properties, each of them—if on the same level of abstraction—is proportionally worth n-1. In other words, a car having brakes or having a gas cap are weighted equally so far as their value goes, so long as both are a part of one's definition of one's personal concept of a "car." Since a gas cap is not normally a part of a car's definition, it would be given no weight. Headlights could be weighed twice, once or not at all depending on how headlights appear in the description of a car. Given a finite set of n properties, a thing is good if it is perceived to have all of the properties, fair if it has more than n/2 of them, average if n/2 of them, and bad if it has fewer than n/2.
Infinite sets of properties
Hartman goes on to consider infinite sets of properties. Hartman claims that according to a theorem of transfinite mathematics, any collection of material objects is at most denumerably infinite. This is not, in fact, a theorem of mathematics, though it would follow from certain assumptions on the nature of the physical universe which cosmologists typically make. Starting from the claim that a person can eventually think of a countable infinity of things, Hartman concludes the intension of man is a denumerably infinite set of predicates; which means that man, according to this first definition, is appropriately to be measured by a denumerable infinity. It is reasonable to assume that we also have a countable infinity of levels of thought, and that therefore we can think of a countable infinity of things using a countable infinity of thought levels, giving us the cardinality of the continuum of thoughts. Hartman thus believes that when one sets out to describe a human individual, a continuum of properties is most fitting and appropriate. He therefore claims the intension of man consists of elements. This is the cardinality, in Hartman's system, of intrinsic value.Further combinations are possible, leading to larger uncountable infinities; and Hartman also introduces the reciprocals of aleph number
Aleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
s, which play no role in ordinary mathematics, but which Hartman employs as a sort of infinitesimal proportion, and which he contends goes to zero in the limit as the uncountable cardinals become larger. In Hartman's calculus, a Dear John letter
Dear John letter
A "Dear John letter" is a letter written to a husband or boyfriend by his wife or girlfriend to inform him their relationship is over, usually because the author has found another lover. Dear John Letters are often written out of an inability or unwillingness to inform the person face to face...
("we will always be friends") has axiological value
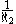, whereas other disvalues such as commercializing the birth of the inspired founder of a religion (e.g., ChristChrist
Christ is the English term for the Greek meaning "the anointed one". It is a translation of the Hebrew , usually transliterated into English as Messiah or Mashiach...
); or making the mistake of taking a metaphor literally; would do slightly better, with a value of
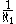.Evaluation of Hartman's work
Hartman invented the Hartman Value Profile, which is however not a description of what is valuable, but a test to determine what people regard as valuable. It measures concept-formation and decision-making capacity. A Hartman festshrift (Values and Valuation) appeared a few years after his death. Some critics would claim that most of the articles in it are not by Hartman supporters. Hartman is out of the mainstream of value philosophy, and is not today regarded as significant among those philosophers who fear (wrongly) that they would be out of work since his goal is to usher value theory out of philosophy and into science. Almost all philosophers would dispute the idea that the number of properties of a thing can in any meaningful way be enumerated, which is something Hartman never said was necessary, and thus they are committing the straw manStraw man
A straw man is a component of an argument and is an informal fallacy based on misrepresentation of an opponent's position, twisting his words or by means of [false] assumptions...
fallacy when they dispute him on that. A standard argument against enumeration is that new properties can be defined in terms of old ones. Philosophers speak of the problem of organic value as a result of the observation that the value of a whole does not seem to be a mere sum of the value of its parts—which again is something Hartman never claimed. Adding more features, even if each seems to be a good one, can sometimes lead to the overall value going down. In this way we get over-engineered software or the kind of DVD remote control which has too many buttons on it. Hartman holds that "the name (that one puts on a concept) sets the norm" so he would rejoin that a "Remote with too many buttons" is a disvalue.
From a mathematician's point of view, much of Hartman's work in The Structure of Value is rather novel and does not use conventional mathematical methodology, nor axiomatic reasoning, however he later employed the mathematics of topological Hausdorff sets, interpreting them as a model for the value-structure of metaphors, in a paper on Aesthetics.
Hartman, following Georg Cantor, uses infinite cardinalities. He posits—as stipulated definitions—the reciprocals of transfinite cardinal numbers. These, together with the algebraic Laws of Exponents, enables him to construct what is today known as The Calculus of Values. He does not in the STRUCTURE book clearly explain how he calculates the value of such items as Christmas shopping in terms of this calculus, although he does explain it in his paper "The Measurement of Value." While inverses of infinite quantities (infinitesimals) exist in certain systems of numbers, such as hyperreal numbers and surreal numbers, these are not reciprocals of cardinal numbers.
Hartman supporters counter that it is not necessary for properties to be actually enumerated, only that they exist and can correspond bijectively (one-to-one). The attributes in the meaning of a concept only "consist" as stipulations; they don't exist. Questions regarding the actual existence of an exemplar of a concept belong to ontology.
Intensional attributes can resemble, but are not identical to, the properties perceived by the five senses. Attributes are names of properties. When, even partially, the properties of a thing match the attributes of that thing in the mind of the one making the judgment, the thing will be said to have "value". When they completely correspond, the thing will be called "good". These are basic ideas in value science.