
Second partial derivative test
Encyclopedia
In mathematics
, the second partial derivative test is a method in multivariable calculus
used to determine if a critical point
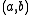 of a function
of a function 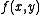 is a minimum, maximum or saddle point
is a minimum, maximum or saddle point
.
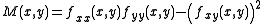
or in other words the determinant
of a 2×2 Hessian matrix
,
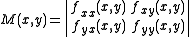 .
.
This analysis applies only to a function of two variables. For a function of more variables, one must look at the eigenvalues of the Hessian matrix at the critical point. The following test can be applied at a non-degenerate critical point x. If the Hessian is positive definite at x, then f attains a local minimum at x. If the Hessian is negative definite at x, then f attains a local maximum at x. If the Hessian has both positive and negative eigenvalues then x is a saddle point for f (this is true even if x is degenerate). Otherwise the test is inconclusive. Note that for functions of three or more variables, the determinant of the Hessian does not provide enough information to classify the critical point. Note also that this statement of the second derivative test for many variables also applies in the two-variable and one-variable case. In the latter case, we recover the usual second derivative test
.
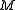 and
and 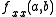 are the leading principal minors of the Hessian. The conditions listed above (the sign of these values) are the conditions for the definiteness of the Hessian.
are the leading principal minors of the Hessian. The conditions listed above (the sign of these values) are the conditions for the definiteness of the Hessian.
We only test values for which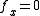 and
and 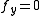 . This is because the function, on its traces in the xz-plane and the yz-plane, have its derivative equal to zero.
. This is because the function, on its traces in the xz-plane and the yz-plane, have its derivative equal to zero.
If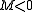 then
then 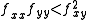 . If
. If 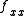 and
and 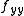 have different signs, then one must be positive and the other must be negative. Thus the concavities of the x cross section (the yz trace) and the y cross section (the xz trace) are in opposite direction. This is clearly a saddle point.
have different signs, then one must be positive and the other must be negative. Thus the concavities of the x cross section (the yz trace) and the y cross section (the xz trace) are in opposite direction. This is clearly a saddle point.
If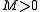 then
then 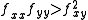 , which implies that
, which implies that 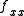 and
and 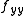 are the same sign and sufficiently large. For this case the concavities of the x and y cross sections are either both up if positive, or both down if negative. This is clearly a local minimum or a local maximum, respectively.
are the same sign and sufficiently large. For this case the concavities of the x and y cross sections are either both up if positive, or both down if negative. This is clearly a local minimum or a local maximum, respectively.
This leaves the last case of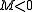 — so
— so 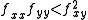 — and
— and  and
and 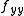 having the same sign. The geometric interpretation of what is happening here is that since
having the same sign. The geometric interpretation of what is happening here is that since 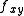 is large it means the slope of the graph in one direction is changing rapidly as we move in the orthogonal direction and overcoming the concavity of the orthogonal direction. So for example, let's take the case of all second derivatives are positive and (a,b) = (0,0). In the case of M > 0 it would mean that any direction in the xy plane we move from the origin, the value of the function increases--a local minimum. In the M < 0 case (
is large it means the slope of the graph in one direction is changing rapidly as we move in the orthogonal direction and overcoming the concavity of the orthogonal direction. So for example, let's take the case of all second derivatives are positive and (a,b) = (0,0). In the case of M > 0 it would mean that any direction in the xy plane we move from the origin, the value of the function increases--a local minimum. In the M < 0 case (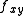 sufficiently large), however, if we move at some direction between the x and y axis into the second quadrant, for example, of the xy plane, then despite the fact that the positive concavity would cause us to expect the value of the function to increase, the slope in the x direction is increasing even faster, which means that as we go left (negative x-direction) into the second quadrant, the value of the function ends up decreasing. Additionally, since the origin is a stationary point by hypothesis, we have a saddle point.
sufficiently large), however, if we move at some direction between the x and y axis into the second quadrant, for example, of the xy plane, then despite the fact that the positive concavity would cause us to expect the value of the function to increase, the slope in the x direction is increasing even faster, which means that as we go left (negative x-direction) into the second quadrant, the value of the function ends up decreasing. Additionally, since the origin is a stationary point by hypothesis, we have a saddle point.

To solve this problem we must first find the first partial derivatives with respect to x and y of the function.
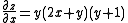
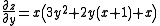
Looking at
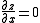
we see that y must equal 0, −1 or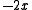 .
.
We plug the first solution y = 0 into the next equation, and get
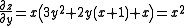
There were other possibilities for y, so for y = -1 we have
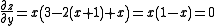
So x must be equal to 1 or 0. For y =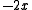 :
:
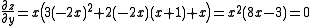
So x must equal 0 or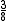 for y = 0 and
for y = 0 and 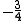 , respectively.
, respectively.
Let's list all the critical values now.
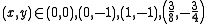
Now we have to label the critical values using the second derivative test.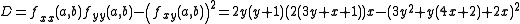
Now we plug in all the different critical values we found to label them.
We have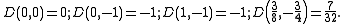
So we can now label some of the points, at (0, −1) and (1, −1) f(x, y) has a saddle point, at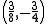 it has a maximum, since
it has a maximum, since 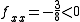 . At the remaining point we need higher order tests to find out what exactly the function is doing.
. At the remaining point we need higher order tests to find out what exactly the function is doing.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the second partial derivative test is a method in multivariable calculus
Multivariable calculus
Multivariable calculus is the extension of calculus in one variable to calculus in more than one variable: the differentiated and integrated functions involve multiple variables, rather than just one....
used to determine if a critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
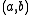 of a function
of a function 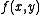 is a minimum, maximum or saddle point
is a minimum, maximum or saddle pointSaddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
.
Explanation
Suppose that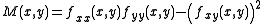
or in other words the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a 2×2 Hessian matrix
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
,
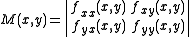 .
.- If
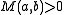 and
and 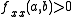 then
then 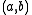 is a local minimum of
is a local minimum of 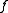 .
. - If
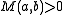 and
and 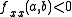 then
then 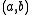 is a local maximum of
is a local maximum of 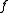 .
. - If
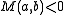 then
then 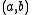 is a saddle pointSaddle pointIn mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
is a saddle pointSaddle pointIn mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
of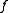 .
. - If
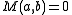 then the second derivatives test is inconclusive.
then the second derivatives test is inconclusive.
This analysis applies only to a function of two variables. For a function of more variables, one must look at the eigenvalues of the Hessian matrix at the critical point. The following test can be applied at a non-degenerate critical point x. If the Hessian is positive definite at x, then f attains a local minimum at x. If the Hessian is negative definite at x, then f attains a local maximum at x. If the Hessian has both positive and negative eigenvalues then x is a saddle point for f (this is true even if x is degenerate). Otherwise the test is inconclusive. Note that for functions of three or more variables, the determinant of the Hessian does not provide enough information to classify the critical point. Note also that this statement of the second derivative test for many variables also applies in the two-variable and one-variable case. In the latter case, we recover the usual second derivative test
Second derivative test
In calculus, the second derivative test is a criterion often useful for determining whether a given stationary point of a function is a local maximum or a local minimum using the value of the second derivative at the point....
.
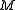 and
and 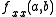 are the leading principal minors of the Hessian. The conditions listed above (the sign of these values) are the conditions for the definiteness of the Hessian.
are the leading principal minors of the Hessian. The conditions listed above (the sign of these values) are the conditions for the definiteness of the Hessian.We only test values for which
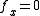 and
and 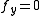 . This is because the function, on its traces in the xz-plane and the yz-plane, have its derivative equal to zero.
. This is because the function, on its traces in the xz-plane and the yz-plane, have its derivative equal to zero.Geometric interpretation
Assuming that all derivatives are evaluated at (a,b), and that the value of the first derivatives vanish there.If
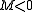 then
then 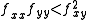 . If
. If 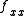 and
and 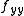 have different signs, then one must be positive and the other must be negative. Thus the concavities of the x cross section (the yz trace) and the y cross section (the xz trace) are in opposite direction. This is clearly a saddle point.
have different signs, then one must be positive and the other must be negative. Thus the concavities of the x cross section (the yz trace) and the y cross section (the xz trace) are in opposite direction. This is clearly a saddle point.If
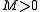 then
then 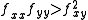 , which implies that
, which implies that 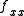 and
and 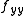 are the same sign and sufficiently large. For this case the concavities of the x and y cross sections are either both up if positive, or both down if negative. This is clearly a local minimum or a local maximum, respectively.
are the same sign and sufficiently large. For this case the concavities of the x and y cross sections are either both up if positive, or both down if negative. This is clearly a local minimum or a local maximum, respectively.This leaves the last case of
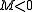 — so
— so 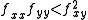 — and
— and  and
and 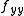 having the same sign. The geometric interpretation of what is happening here is that since
having the same sign. The geometric interpretation of what is happening here is that since 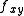 is large it means the slope of the graph in one direction is changing rapidly as we move in the orthogonal direction and overcoming the concavity of the orthogonal direction. So for example, let's take the case of all second derivatives are positive and (a,b) = (0,0). In the case of M > 0 it would mean that any direction in the xy plane we move from the origin, the value of the function increases--a local minimum. In the M < 0 case (
is large it means the slope of the graph in one direction is changing rapidly as we move in the orthogonal direction and overcoming the concavity of the orthogonal direction. So for example, let's take the case of all second derivatives are positive and (a,b) = (0,0). In the case of M > 0 it would mean that any direction in the xy plane we move from the origin, the value of the function increases--a local minimum. In the M < 0 case (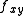 sufficiently large), however, if we move at some direction between the x and y axis into the second quadrant, for example, of the xy plane, then despite the fact that the positive concavity would cause us to expect the value of the function to increase, the slope in the x direction is increasing even faster, which means that as we go left (negative x-direction) into the second quadrant, the value of the function ends up decreasing. Additionally, since the origin is a stationary point by hypothesis, we have a saddle point.
sufficiently large), however, if we move at some direction between the x and y axis into the second quadrant, for example, of the xy plane, then despite the fact that the positive concavity would cause us to expect the value of the function to increase, the slope in the x direction is increasing even faster, which means that as we go left (negative x-direction) into the second quadrant, the value of the function ends up decreasing. Additionally, since the origin is a stationary point by hypothesis, we have a saddle point.Examples
Find and label the critical points of the following function:
To solve this problem we must first find the first partial derivatives with respect to x and y of the function.
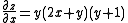
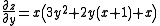
Looking at
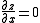
we see that y must equal 0, −1 or
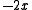 .
.We plug the first solution y = 0 into the next equation, and get
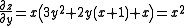
There were other possibilities for y, so for y = -1 we have
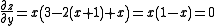
So x must be equal to 1 or 0. For y =
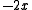 :
: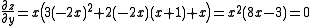
So x must equal 0 or
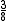 for y = 0 and
for y = 0 and 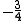 , respectively.
, respectively.Let's list all the critical values now.
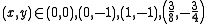
Now we have to label the critical values using the second derivative test.
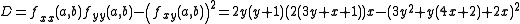
Now we plug in all the different critical values we found to label them.
We have
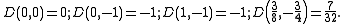
So we can now label some of the points, at (0, −1) and (1, −1) f(x, y) has a saddle point, at
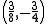 it has a maximum, since
it has a maximum, since 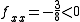 . At the remaining point we need higher order tests to find out what exactly the function is doing.
. At the remaining point we need higher order tests to find out what exactly the function is doing.
