
Segre cubic
Encyclopedia
In algebraic geometry, the Segre cubic is a cubic threefold
embedded in 4 (or sometimes 5) dimensional projective space, studied by .
The Segre cubic is the set of points (x0:x1:x2:x3:x4:x5) of P5 satisfying the equations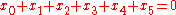
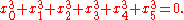
Its intersection with any hyperplane xi = 0 is the Clebsch cubic surface. Its intersection with any hyperplane xi = xj is Cayley's nodal cubic surface
. Its dual is the Igusa quartic
3-fold in P4. Its Hessian is the Barth–Nieto quintic
.
A cubic hypersurface in P4 has at most 10 nodes, and up to isomorphism the Segre cubic is the unique one with 10 nodes. Its nodes are the points conjugate to (1:1:1:−1:−1:−1) under permutations of coordinates.
Cubic threefold
In algebraic geometry, a cubic threefold is a hypersurface of degree 3 in 4-dimensional projective space. Cubic threefolds are all unirational, but used intermediate Jacobians to show that non-singular cubic threefolds are not rational. The space of lines on a non-singular cubic 3-fold is a...
embedded in 4 (or sometimes 5) dimensional projective space, studied by .
The Segre cubic is the set of points (x0:x1:x2:x3:x4:x5) of P5 satisfying the equations
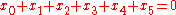
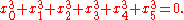
Its intersection with any hyperplane xi = 0 is the Clebsch cubic surface. Its intersection with any hyperplane xi = xj is Cayley's nodal cubic surface
Cayley's nodal cubic surface
In algebraic geometry, the Cayley surface,named after Arthur Cayley, is a cubic surface in 3-dimensional projective space with four conical points. It can be given by the equation wxy+ xyz+ yzw+zwx =0\...
. Its dual is the Igusa quartic
Igusa quartic
In algebraic geometry, the Igusa quartic is a quartic hypersurface in 4-dimensional projective space, studied by .It is closely related to the moduli space of genus 2 curves with level 2 structure. It is the dual of the Segre cubic....
3-fold in P4. Its Hessian is the Barth–Nieto quintic
Barth–Nieto quintic
In algebraic geometry, the Barth–Nieto quintic is a quintic 3-fold in 4 dimensional projective space studied by that is the Hessian of the Segre cubic...
.
A cubic hypersurface in P4 has at most 10 nodes, and up to isomorphism the Segre cubic is the unique one with 10 nodes. Its nodes are the points conjugate to (1:1:1:−1:−1:−1) under permutations of coordinates.

