Seifert conjecture
Encyclopedia
In mathematics
, the Seifert conjecture states that every nonsingular, continuous vector field
on the 3-sphere
has a closed orbit. It is named after Herbert Seifert
. In a 1950 paper, Seifert asked if such a vector field exists, but did not phrase non-existence as a conjecture. He also established the conjecture for perturbations of the Hopf fibration.
The conjecture was disproven in 1974 by Paul Schweitzer, who exhibited a
counterexample. Schweitzer's construction was then modified by Jenny Harrison
in 1988 to make a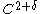
counterexample for some 
. The existence of smoother counterexamples remained an open question until 1993 when Krystyna Kuperberg constructed a very different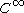 
counterexample. Later this construction was shown to have real analytic and piecewise linear versions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Seifert conjecture states that every nonsingular, continuous vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
on the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
has a closed orbit. It is named after Herbert Seifert
Herbert Seifert
Herbert Karl Johannes Seifert was a German mathematician known for his work in topology....
. In a 1950 paper, Seifert asked if such a vector field exists, but did not phrase non-existence as a conjecture. He also established the conjecture for perturbations of the Hopf fibration.
The conjecture was disproven in 1974 by Paul Schweitzer, who exhibited a
counterexample. Schweitzer's construction was then modified by Jenny HarrisonJenny Harrison
Jenny Harrison is a professor of mathematics at UC Berkeley. She specializes in geometric analysis and areas in the intersection of algebra, geometry, and geometric measure theory...
in 1988 to make a
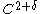counterexample for some . The existence of smoother counterexamples remained an open question until 1993 when Krystyna Kuperberg constructed a very different 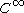counterexample. Later this construction was shown to have real analytic and piecewise linear versions.Further reading
- K. Kuperberg, Aperiodic dynamical systems. Notices Amer. Math. Soc. 46 (1999), no. 9, 1035--1040.