
Semi-infinite
Encyclopedia
The term semi-infinite has several related meanings in various branches of pure and applied mathematics
. It typically describes objects which are infinite or unbounded in some but not all possible ways.
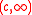 and
and 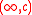 and their closed counterparts are semi-infinite subsets of
and their closed counterparts are semi-infinite subsets of  . Half-space
. Half-space
s are sometimes described as semi-infinite regions.
Semi-infinite regions occur frequently in the study of differential equations. For instance, one might study solutions of the heat equation in an idealised semi-infinite metal bar.
A semi-infinite integral
is an improper integral
over a semi-infinite interval. More generally, objects indexed or parametrised by semi-infinite sets may be described as semi-infinite.
Most forms of semi-infiniteness are boundedness properties, not cardinality or measure
properties: semi-infinite sets are typically infinite in cardinality and measure.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. It typically describes objects which are infinite or unbounded in some but not all possible ways.
In ordered structures and Euclidean spaces
Generally, a semi-infinite set is bounded in one direction, and unbounded in another. For instance, the natural numbers are semi-infinite considered as a subset of the integers; similarly, the intervalsInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
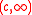 and
and 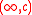 and their closed counterparts are semi-infinite subsets of
and their closed counterparts are semi-infinite subsets of  . Half-space
. Half-spaceHalf-space
In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
s are sometimes described as semi-infinite regions.
Semi-infinite regions occur frequently in the study of differential equations. For instance, one might study solutions of the heat equation in an idealised semi-infinite metal bar.
A semi-infinite integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
is an improper integral
Improper integral
In calculus, an improper integral is the limit of a definite integral as an endpoint of the interval of integration approaches either a specified real number or ∞ or −∞ or, in some cases, as both endpoints approach limits....
over a semi-infinite interval. More generally, objects indexed or parametrised by semi-infinite sets may be described as semi-infinite.
Most forms of semi-infiniteness are boundedness properties, not cardinality or measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
properties: semi-infinite sets are typically infinite in cardinality and measure.

