Senary
Encyclopedia
In mathematics
, a senary numeral system
is a base- numeral system.
Senary may be considered useful in the study of prime number
s since all primes other than 2 and 3, when expressed in base-six, have 1 or 5 as the final digit. Writing out the prime numbers in base-six (and using the subscript 6 to denote that these are senary numbers), the first few primes are
That is, for every prime number p with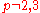
, one has the modular arithmetic
relations that either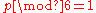
or 
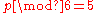: the final digits is a 1 or a 5. This is proved by contradiction.
For integer n:
Furthermore, all known perfect number
s besides 6 itself have 44 as the final two digits when expressed in base 6.
Each regular human hand may be said to have six unambiguous positions; a fist, one finger (or thumb) extended, two, three, four and then all five extended.
If the right hand is used to represent a unit, and the left to represent the 'sixes', it becomes possible for one person to represent the values from zero to 55senary (35decimal) with their fingers, rather than the usual ten obtained in standard finger counting. e.g. if three fingers are extended on the left hand and four on the right, 34senary is represented. This is equivalent to 3 × 6 + 4 which is 22decimal.
Which hand is used for the 'sixes' and which the units is down to preference on the part of the counter, however when viewed from the counter's perspective, using the left hand as the most significant digit correlates with the written representation of the same senary number.
Other finger counting
systems, such as chisanbop or finger binary
, allow counting to 99 or even 1,023.
of the first two prime number
s and is adjacent to the next two prime numbers, many senary fractions have simple representations:
( represents an infinitely repeating digit, or sequence of digits.)
is reported to have senary numerals. Mer means 6, mer an thef means 6×2 = 12, nif means 36, and nif thef means 36×2 = 72.
Proto-Uralic
is also suspected to have used senary numerals.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a senary numeral system
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
is a base- numeral system.
Senary may be considered useful in the study of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s since all primes other than 2 and 3, when expressed in base-six, have 1 or 5 as the final digit. Writing out the prime numbers in base-six (and using the subscript 6 to denote that these are senary numbers), the first few primes are
That is, for every prime number p with
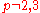, one has the modular arithmeticModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
relations that either
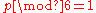or 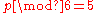: the final digits is a 1 or a 5. This is proved by contradiction.For integer n:
- If n mod 6 = 0, 6|n
- If n mod 6 = 2, 2|n
- If n mod 6 = 3, 3|n
- If n mod 6 = 4, 2|n
Furthermore, all known perfect number
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
s besides 6 itself have 44 as the final two digits when expressed in base 6.
Finger counting
| 1 | 2 | 3 | 4 | 5 | 10 |
|---|---|---|---|---|---|
| 2 | 4 | 10 | 12 | 14 | 20 |
| 3 | 10 | 13 | 20 | 23 | 30 |
| 4 | 12 | 20 | 24 | 32 | 40 |
| 5 | 14 | 23 | 32 | 41 | 50 |
| 10 | 20 | 30 | 40 | 50 | 100 |
Each regular human hand may be said to have six unambiguous positions; a fist, one finger (or thumb) extended, two, three, four and then all five extended.
If the right hand is used to represent a unit, and the left to represent the 'sixes', it becomes possible for one person to represent the values from zero to 55senary (35decimal) with their fingers, rather than the usual ten obtained in standard finger counting. e.g. if three fingers are extended on the left hand and four on the right, 34senary is represented. This is equivalent to 3 × 6 + 4 which is 22decimal.
Which hand is used for the 'sixes' and which the units is down to preference on the part of the counter, however when viewed from the counter's perspective, using the left hand as the most significant digit correlates with the written representation of the same senary number.
Other finger counting
Finger counting
Finger counting, or dactylonomy, is the art of counting along one's fingers. Though marginalized in modern societies by Arabic numerals, formerly different systems flourished in many cultures, including educated methods far more sophisticated than the one-by-one finger count taught today in...
systems, such as chisanbop or finger binary
Finger binary
Finger binary is a system for counting and displaying binary numbers on the fingers and thumbs of one or more hands. It is possible to count from 0 to 31 using the fingers of a single hand, or from 0 through 1023 if both hands are used.- Mechanics :In the binary number system, each numerical...
, allow counting to 99 or even 1,023.
Fractions
Because six is the productProduct (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of the first two prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s and is adjacent to the next two prime numbers, many senary fractions have simple representations:
| Decimal | Senary | ||
|---|---|---|---|
| 1/2 | 0.5 | 1/2 | 0.3 |
| 1/3 | 0. | 1/3 | 0.2 |
| 1/4 | 0.25 | 1/4 | 0.13 |
| 1/5 | 0.2 | 1/5 | 0. |
| 1/6 | 0.1 | 1/10 | 0.1 |
| 1/7 | 0. | 1/11 | 0.0 |
| 1/8 | 0.125 | 1/12 | 0.043 |
| 1/9 | 0. | 1/13 | 0.04 |
| 1/10 | 0.1 | 1/14 | 0.0 |
| 1/11 | 0.0 | 1/15 | 0.0 |
| 1/12 | 0.08 | 1/20 | 0.03 |
| 1/13 | 0.0 | 1/21 | 0.0 |
| 1/14 | 0.0 | 1/22 | 0.0 |
| 1/15 | 0.0 | 1/23 | 0.0 |
| 1/16 | 0.0625 | 1/24 | 0.0213 |
| 1/18 | 0.0 | 1/30 | 0.02 |
( represents an infinitely repeating digit, or sequence of digits.)
Natural languages
The Ndom language of Papua New GuineaPapua New Guinea
Papua New Guinea , officially the Independent State of Papua New Guinea, is a country in Oceania, occupying the eastern half of the island of New Guinea and numerous offshore islands...
is reported to have senary numerals. Mer means 6, mer an thef means 6×2 = 12, nif means 36, and nif thef means 36×2 = 72.
Proto-Uralic
Proto-Uralic language
Proto-Uralic is the hypothetical language ancestral to the Uralic language family. The language was originally spoken in a small area in about 7000-2000 BC , and expanded to give differentiated protolanguages. The exact location of the area or Urheimat is not known, but the vicinity of the Ural...
is also suspected to have used senary numerals.
See also
- DicewareDicewareDiceware is a method for creating passphrases, passwords, and other cryptographic variables using ordinary dice as a hardware random number generator. For each word in the passphrase, five dice rolls are required. The numbers that come up in the rolls are assembled as a five digit number, e.g....
has a way of encoding base 6 values into pronounceable words, using a standardized list of 7,776 distinct words
Closely related number systems
- DuodecimalDuodecimalThe duodecimal system is a positional notation numeral system using twelve as its base. In this system, the number ten may be written as 'A', 'T' or 'X', and the number eleven as 'B' or 'E'...
(base 12) - Trigesimal (Base 30Base 30Base 30 or trigesimal is a positional numeral system using 30 as the radix. Digits in this base can be represented using the Arabic numerals 0-9 and the Latin letters A-T....
) - Base 36Base 36Base 36 is a positional numeral system using 36 as the radix. The choice of 36 is convenient in that the digits can be represented using the Arabic numerals 0-9 and the Latin letters A-Z...
External links
- Shack's Base Six Dialectic
- Senary Base Conversion, includes fractional part, from Math Is Fun
- MathService, ConvertBase .NET web service